Decision Trees¶

Trees, Forests & Ensembles¶

02/17/20

Andreas C. Müller

FIXME missing value treatment in trees FIXME: saw 1d tree explanation somewhere that was really neat? regression? FIXME show how everything is axis parallel and how that makes it hard to learn linear things FIXME show that only rank is important FIXME bullet points! FIXME oblique trees? animation searching for split in tree? predition animation tree? extra tree: only one thereshold per feature? FIXME: bias variance plot replace by two kinds of error (approximation, generalization) FIXME: length actually good. so more of a note than fixme lol FIXME: test curve mislabeled warm start FIXME explain “values” in figure in slide notes FIXME plots sometimes say values and sometimes samples, make sure it’s consistent! FIXME some plots say entropy but actually use gini?! wtf, redo plots FIXME add graphviz back in as it’s a bit higher quality? FIXME add example of subset splits with categorical features FIXME don’t do warm starts and OOB and do better explanations of rest FIXME entropy calculation for tree, maybe do it once explicitly? FIXME Go over finding a single split in some toy data! 1d regression? FIXME order is a bit weight FIXME better example of CCP helping FIXME show averaging in forest on regression example?

Why Trees?¶

Trees are really very powerful models both for classification and regression, they’re very commonly used. Trees are very popular in the industry. Only beaten by deep neural networks. Tree-based models are one of the main tools in the toolbox of most machine learning practitioners.

Trees really don’t care about the scale of the data so you don’t really have to do a lot of preprocessing. Trees don’t care about the distribution of your data. There are versions of trees that can deal with categorical variables and with missing values. By combining multiple trees you can build stronger models.

Very powerful modeling method – non-linear!
Doesn’t care about scaling of distribution of data!
“Interpretable”
Basis of very powerful models!
add stacking classifier from PR?

Decision Trees for Classification¶

Idea: series of binary questions¶

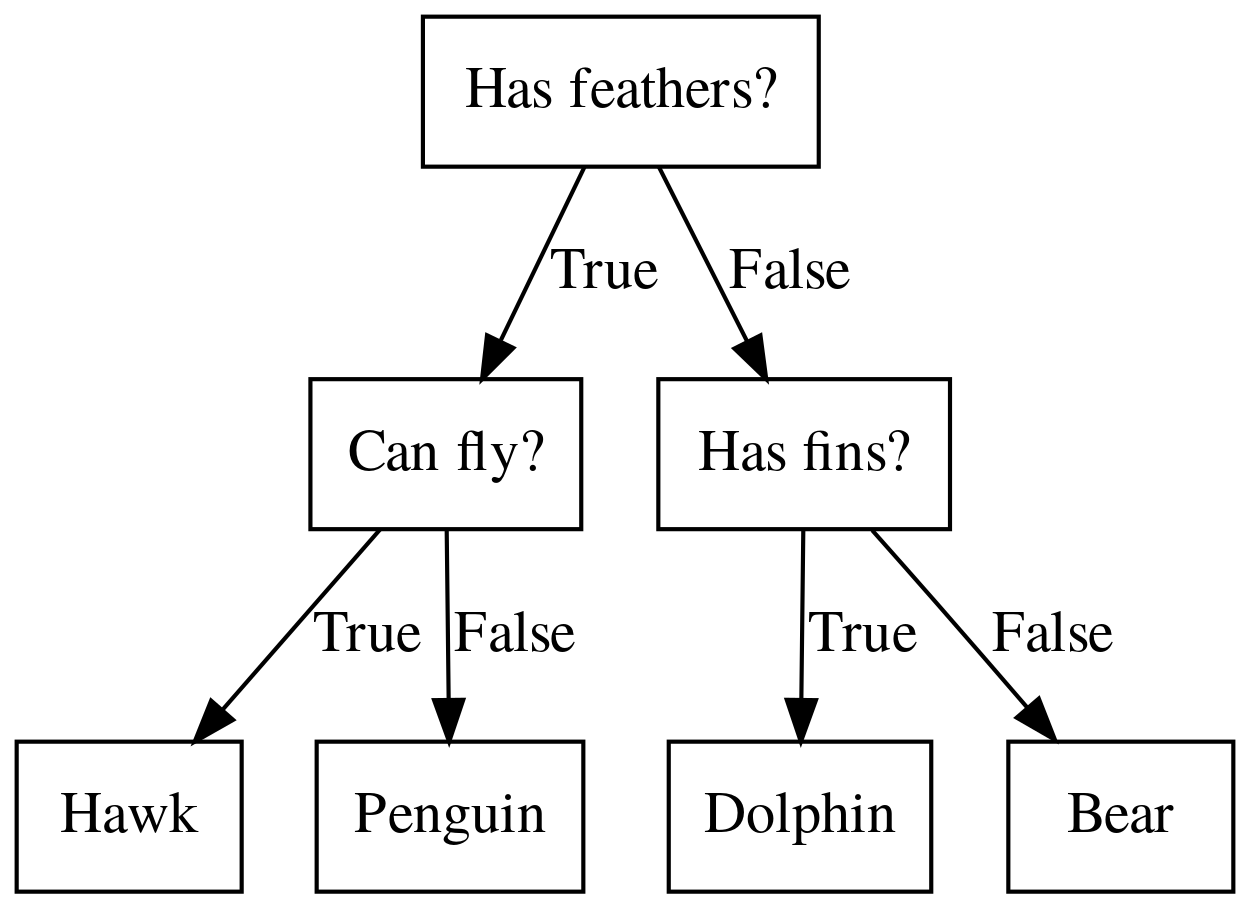
.center[ :scale 70% ]

Binary classification trees are binary trees, where each node corresponds to a question asked about the data. This example is a fictional task where you want to distinguish hawks, penguins, dolphins, and bears. You ask a series of binary questions that will lead to which animal it might be.

Depending on what the answer is for a particular question, you could ask another question. This way you can narrow it down for possible outcomes. Usually, when we are doing classification we have continuous features and so the questions are thresholds on single features.

Building Trees¶

.left-column[ :scale 100%

Continuous features:

“questions” are thresholds on single features.
Minimize impurity ] .right-column[

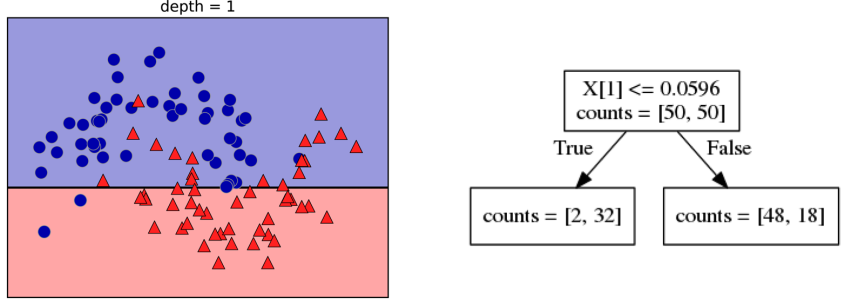
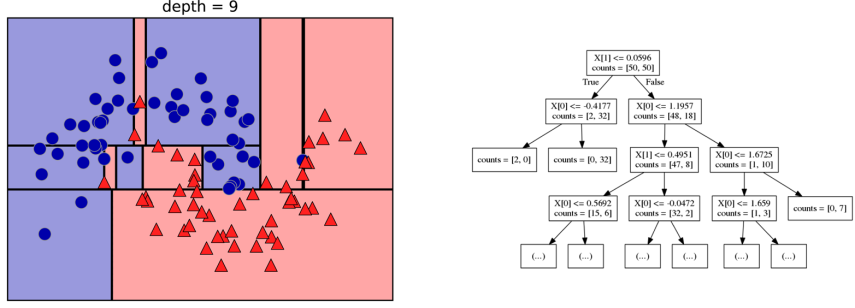
:scale 100% ]

Here is an example of a tree with depth one, that’s basically just thresholding a single feature. In this example, the question being asked is, is X1 less than or equal to 0.0596. The boundary between the 2 regions is the decision boundary. The decision for each of the region would be the majority class on it. This decision tree of depth one would classify everything that is below the horizontal line as class red since there are more red points (32>2) and everything above as blue since there are more blue points (48>18).

The way this threshold was chosen, the way that tree of depth one was learned was to find the best feature and the best threshold to minimize impurity. Which means it tries to make the resulting subsets, the top half and the bottom half here, to be as pure as possible (to consist mostly of one class)

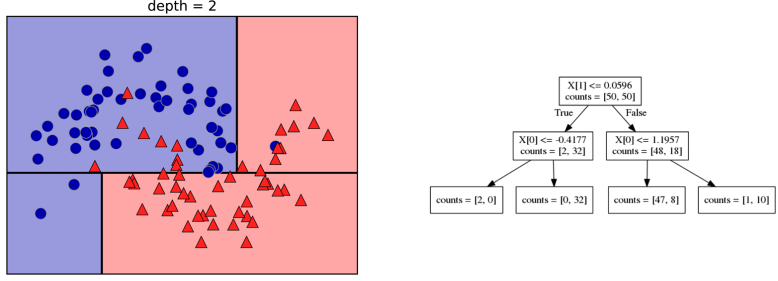
Basically, we’re searching over all possible features and all possible thresholds. Possible thresholds are all values of the feature that we’re observing. So I would start iterating over the first feature and for the first feature, I would look at all possible thresholds and see if this is a good question to ask, i.e. is this a good way to split the data set into two classes.

If you search over all possible features, then the best split is found. Once we find this split, we can then basically apply this algorithm recursively to the two areas that the split created. For top area here, we can ask what the best feature is and what the best threshold for this feature is to make the resulting regions as pure as possible.

Here in the bottom, it asks is X0 less or equal than minus 0.4? The model will predict accordingly, either blue or red. If only one class remain after a split, the tree will not add any splits since the regions have become pure. Each node corresponds to a split and the leaves correspond to regions. All tree building algorithms start greedily building a tree, so they don’t really go back and revisit because it would be too computationally expensive.

Does the layout look okay??

Criteria (for classification)¶

Gini Index:

\[H_\text{gini}(X_m) = \sum_{k\in\mathcal{Y}} p_{mk} (1 - p_{mk})\]

Cross-Entropy:

\[H_\text{CE}(X_m) = -\sum_{k\in\mathcal{Y}} p_{mk} \log(p_{mk})\]

$X_m$ observations in node m

$\mathcal{Y}$ classes

$p_{m\cdot}$ distribution over classes in node m

For classification, there are two common criteria to preserve the purity of the leaf. One is called the Gini Index and the other one is Cross-Entropy.

Gini Index works well in practices. Cross-Entropy is the entropy of the distribution over classes. You want to minimize the entropy over the classes, you want to have a very spike distribution in the classes, you want mostly to be one class and less of the others so that the trees are very certain about what the class is for each leaf.

Prediction¶

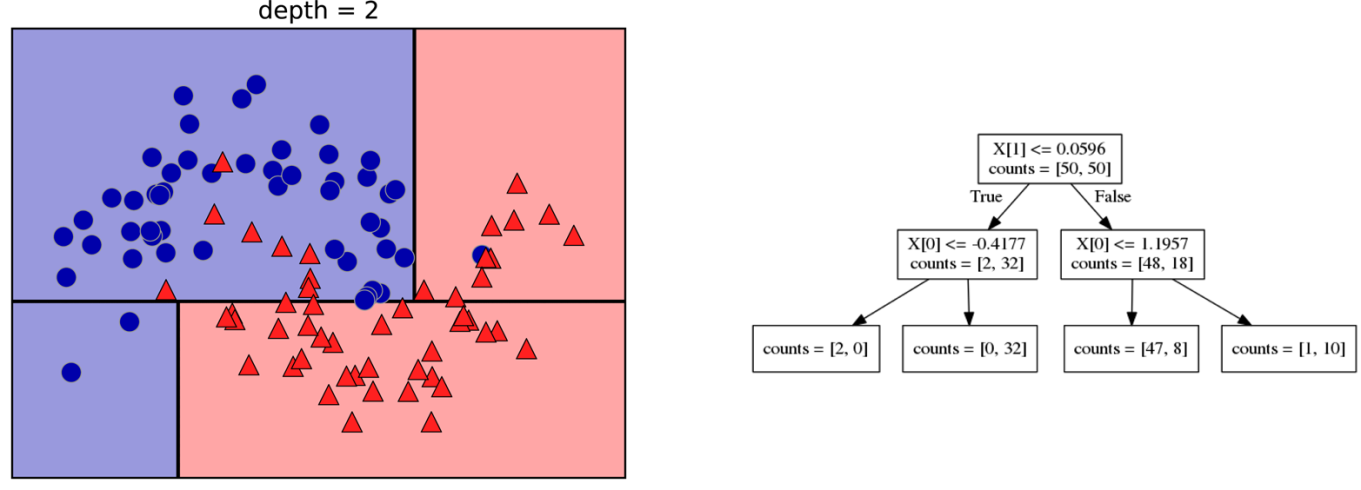
.center[ :scale 80% ]

To make a prediction, I traverse the tree I ask all the questions in the node that I encounter and then I can predict the majority class in the leaf. One thing that’s nice about this is this prediction is really, really fast since this tree is not very deep.

Traverse tree based on feature tests
Predict most common class in leaf

Regression trees¶

\[\text{Prediction: } \bar{y}_m = \frac{1}{N_m} \sum_{i \in N_m} y_i \]

Mean Squared Error: $$ H(X_m) = \frac{1}{N_m} \sum_{i \in N_m} (y_i - \bar{y}_m)^2 $$

Mean Absolute Error: $$ H(X_m) = \frac{1}{N_m} \sum_{i \in N_m} |y_i - \bar{y}_m| $$

You can do the same thing also for regression. In regression, the prediction is usually the mean over the target targets in a leaf. The impurity criteria that I minimized is usually the mean squared error. Basically, you look at how good of a prediction is the mean if I split like this. For each possible split, you can compute the mean for the two resulting nodes and you compute how well the mean in this leaf predicts.

You can use the mean absolute error, if you want it to be more robust outliers then you don’t penalize with the square norm, you only penalize with the L1 norm.

One thing about the regression trees is that they have more tendency to get very deep if you don’t restrict them. Because usually in regression, all targets are distinct, they’re distinct float numbers. So if you want all leaves to be pure, then all of these will have only one node in them, unless you have a special case where you have equal flow numbers as a target, which is not common.

Another thing that’s really nice about trees is that you can visualize them and you can look at them, and you can possibly even explain to your boss what they mean.

Without regularization / pruning:
Each leaf often contains a single point to be “pure”

Visualizing trees with sklearn¶

.smaller[

from sklearn.datasets import load_breast_cancer
cancer = load_breast_cancer()
X_train, X_test, y_train, y_test = train_test_split(cancer.data,cancer.target,
                                                    stratify=cancer.target,
                                                    random_state=0)


from sklearn.tree import DecisionTreeClassifier
tree = DecisionTreeClassifier(max_depth=2)
tree.fit(X_train, y_train)

]

The first way to visualize tree in scikit-learn is a little bit tricky. The second one is a one I hacked.

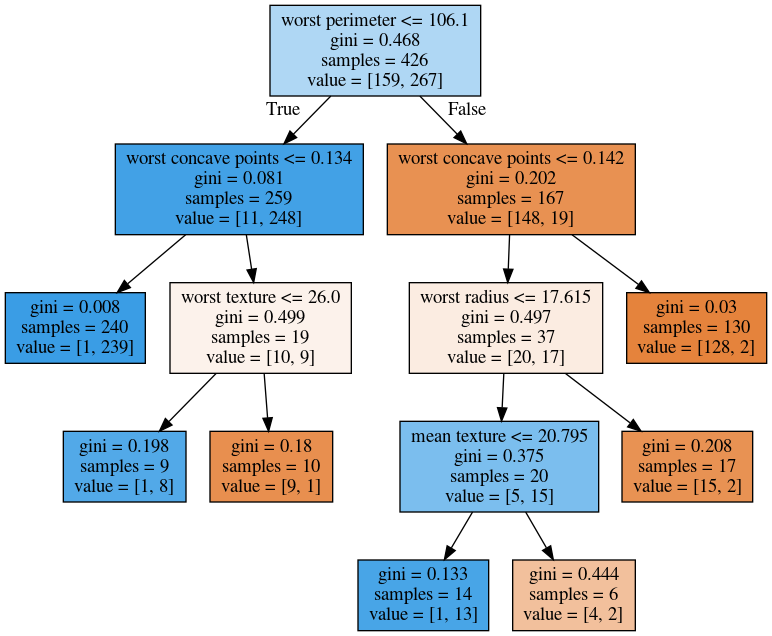
I’m going to use the breast cancer data center, which does the classification of breast tissues. So trees can do much more complicated things than multiclass. For the ease of visualization, I’m going to do binary.

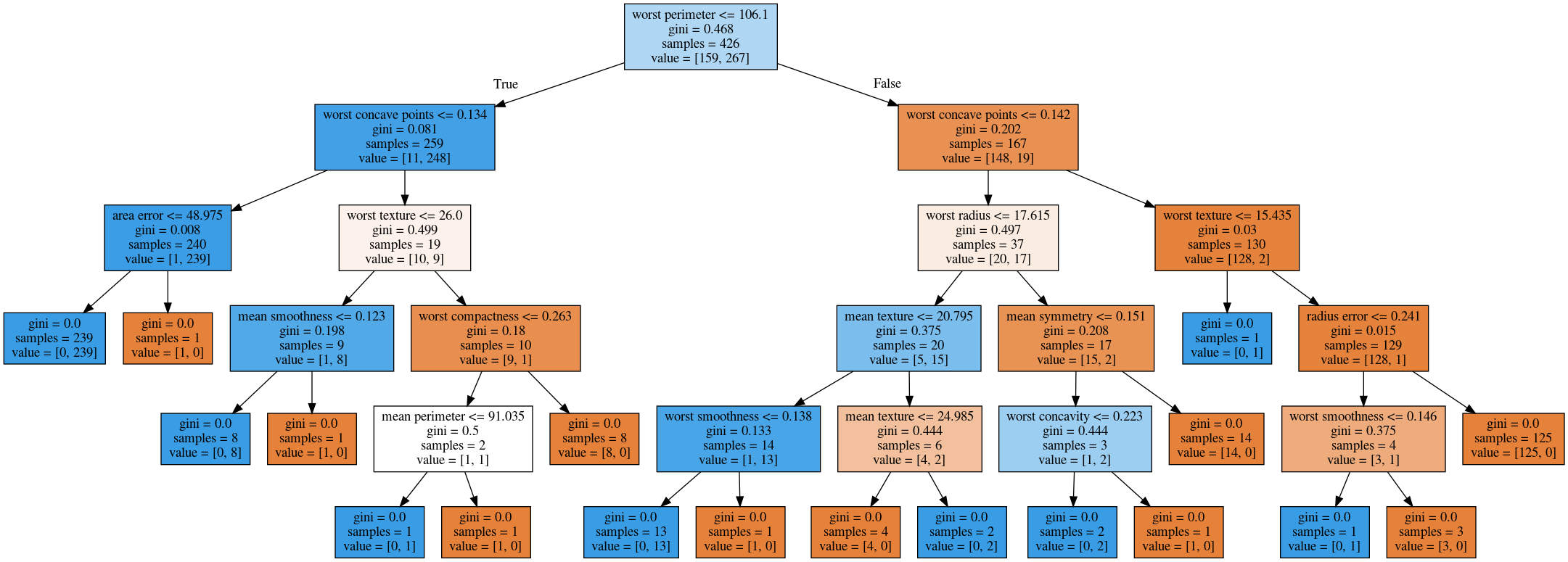
I can build the decision tree classifier, and there’s a method in scikit-learn called export _graphviz, which is basically a file format and the layout engine for showing graphs.

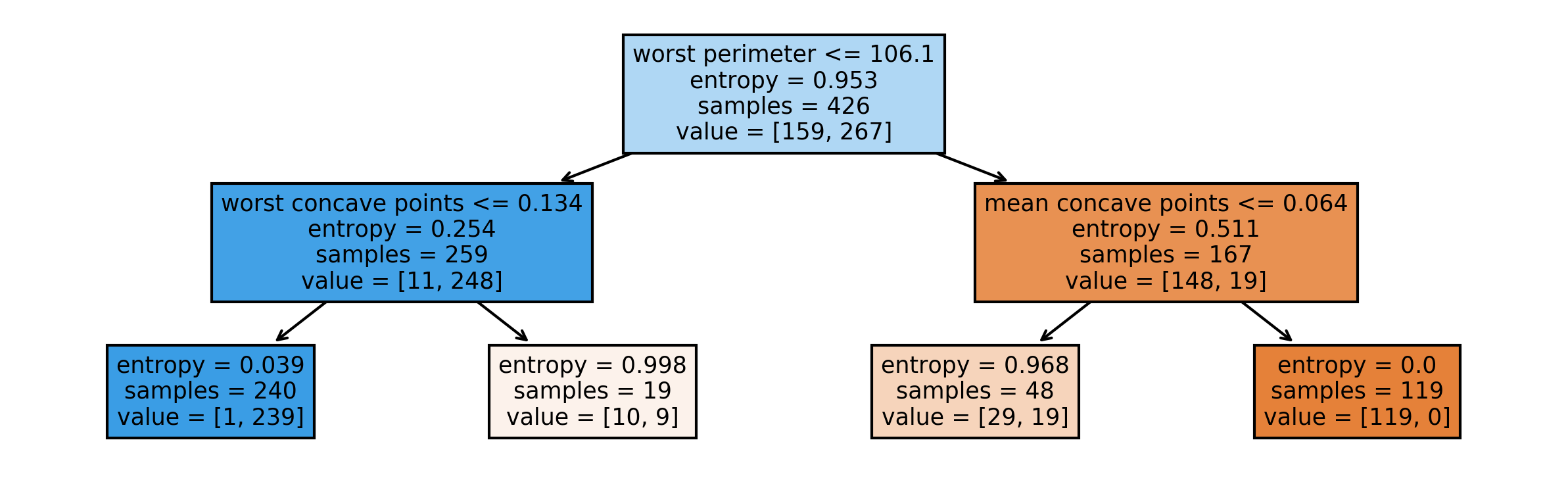
So you can take the tree, the estimator that’s the tree. You can also give it the feature names if you want. You can either write this to a file, or you can get back to string in this dot language. And that’s what it looks like. This is a tree of depth 2 and I gave it the feature names.

Visualizing trees with sklearn¶

from sklearn.tree import plot_tree
tree_dot = plot_tree(tree, feature_names=cancer.feature_names)

.center[ :scale 80% ]

The other thing that I like to use which is easier is this pull request or there’s a gist that you download, it’s a single file called the tree_plotting. And that uses math plot to plot the trees.

Here, at the top you can see the test, then you can see the criteria, then the number of samples in this node and then which class the samples belong to. In the original breast cancer dataset, the top node corresponds to the whole dataset. The tree gets purer and purer as you move down the tree.

Parameter Tuning¶

Pre-pruning vs post-pruning
Pre-pruning: Limit tree size (pick one, maybe two):
- max_depth
- max_leaf_nodes
- min_samples_split
- min_impurity_decrease
- …
I want to talk a little bit about the different parameters that you can choose. Most of the tree growing algorithms are greedy. There are two ways to restrict the growth of the tree after you train them. There are pre-pruning and post-pruning.

In pre-pruning, you restrict while you’re growing. In post-pruning, you build the whole tree (greedily) and then you possibly merge notes. So you possibly undo sort of bad decisions that you made, but you don’t restructure the tree.

In scikit-learn right now, there’s only pre-pruning. The most commonly used criteria are the maximum depth of the tree, the maximum number of leaf nodes, the minimum samples in a node split and minimum decrease impurity.

No pruning¶

.center[ :scale 100% ]

Here’s the full tree for the same dataset.

max_depth = 4¶

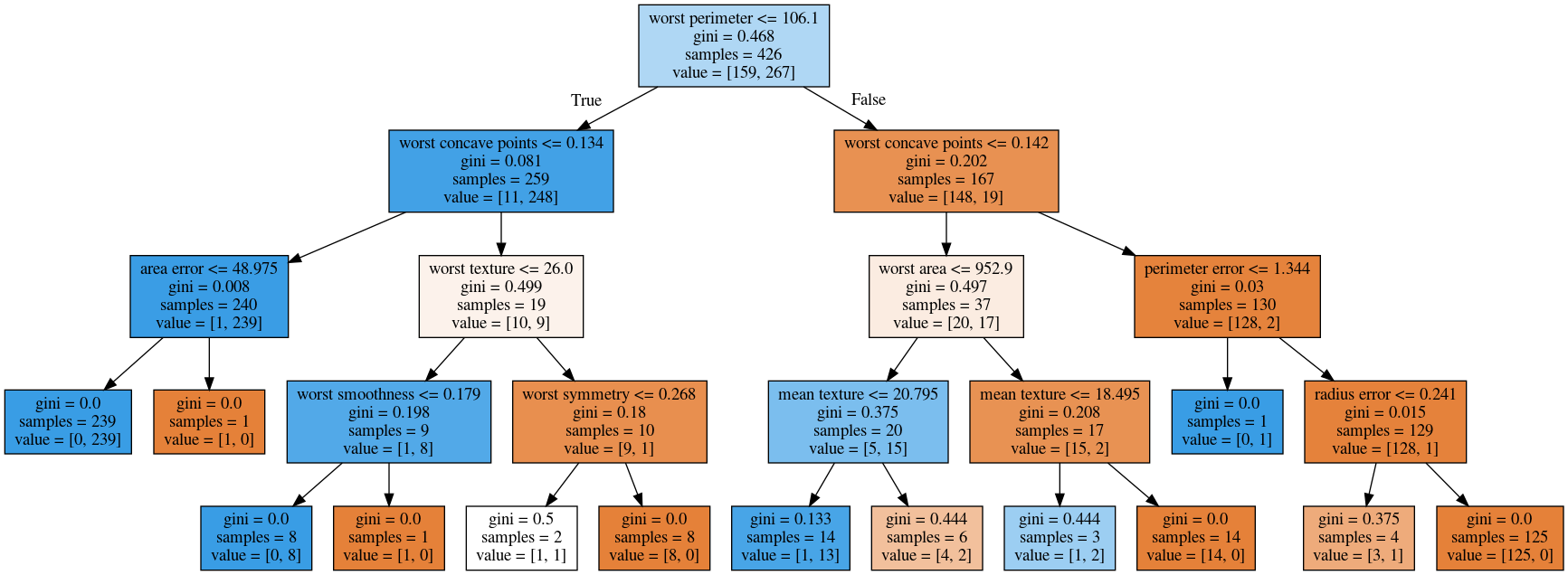
.center[ :scale 100% ]

Maximum depth of the tree restricted to 4. This is like a very simple way. If you are actually building just a single decision tree, this might not be the best way because for example, here you split away the single point which might not be great and other leaves are very mixed. So you can’t make a good prediction here. Since it puts the same depth limit on everywhere in the tree, this is not very fine grained.

What it does is it means that your predictions will be very fast because you never have to go very deep in the tree. It also makes the tree size very small. If you built a lot of trees, you might get issues with the RAM. If you have a lot of very deep trees, they will at some point be bigger than your RAM, and you’ll run into troubles, or if they’re very deep, it might be very slow to predict at some point. So this is a way to restrict how much memory and how much prediction time you’re willing to give.

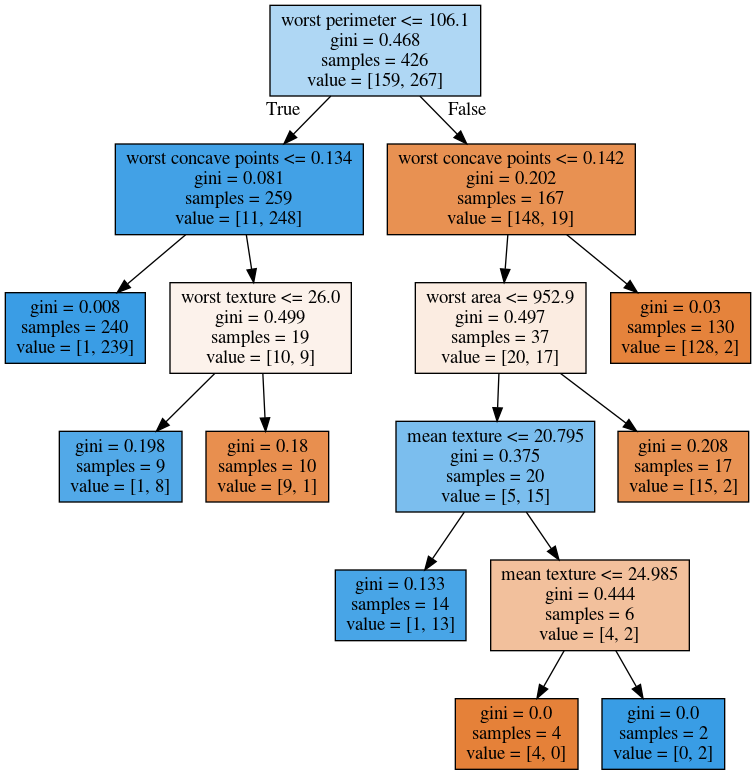
max_leaf_nodes = 8¶

.center[ :scale 50% ]

If you use max_leaf_nodes, it will always put the one that has the greatest impurity decrease first. You can see that in different parts of the trees, there’s different depth. It will prioritize the ones that decrease the impurity the most.

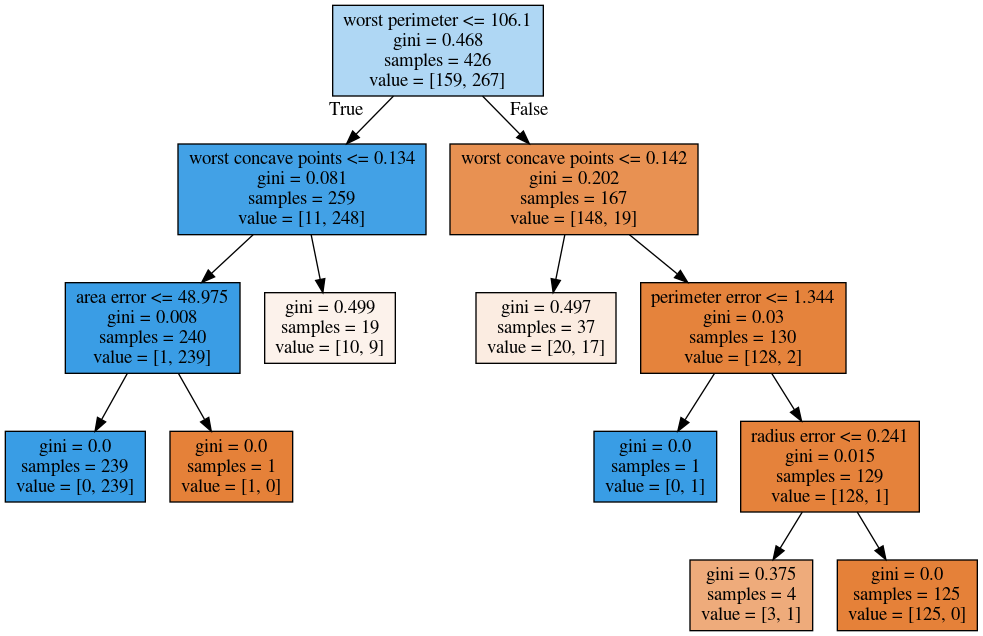
min_samples_split = 50¶

.center[ :scale 70% ]

Min_samples_split is quite simple, it just says only split nodes that have this many samples on them. What I don’t like about this criterion set here, for example, it splits off a single point, which I don’t think is really great, because it’s not going to improve the prediction very much.

So both the max leaf nodes and the minimum impurity decrease will allow you to basically get rid of these very small leaves that don’t really add anything to the prediction.

Impurity decrease will only make splits that decrease the impurity by X amount.

If you want to tune this, you pick one of these and then you just tune this one parameter.

.smaller[

from sklearn.model_selection import GridSearchCV
param_grid = {'max_depth':range(1, 7)}
grid = GridSearchCV(DecisionTreeClassifier(random_state=0),
                    param_grid=param_grid, cv=10)
grid.fit(X_train, y_train)

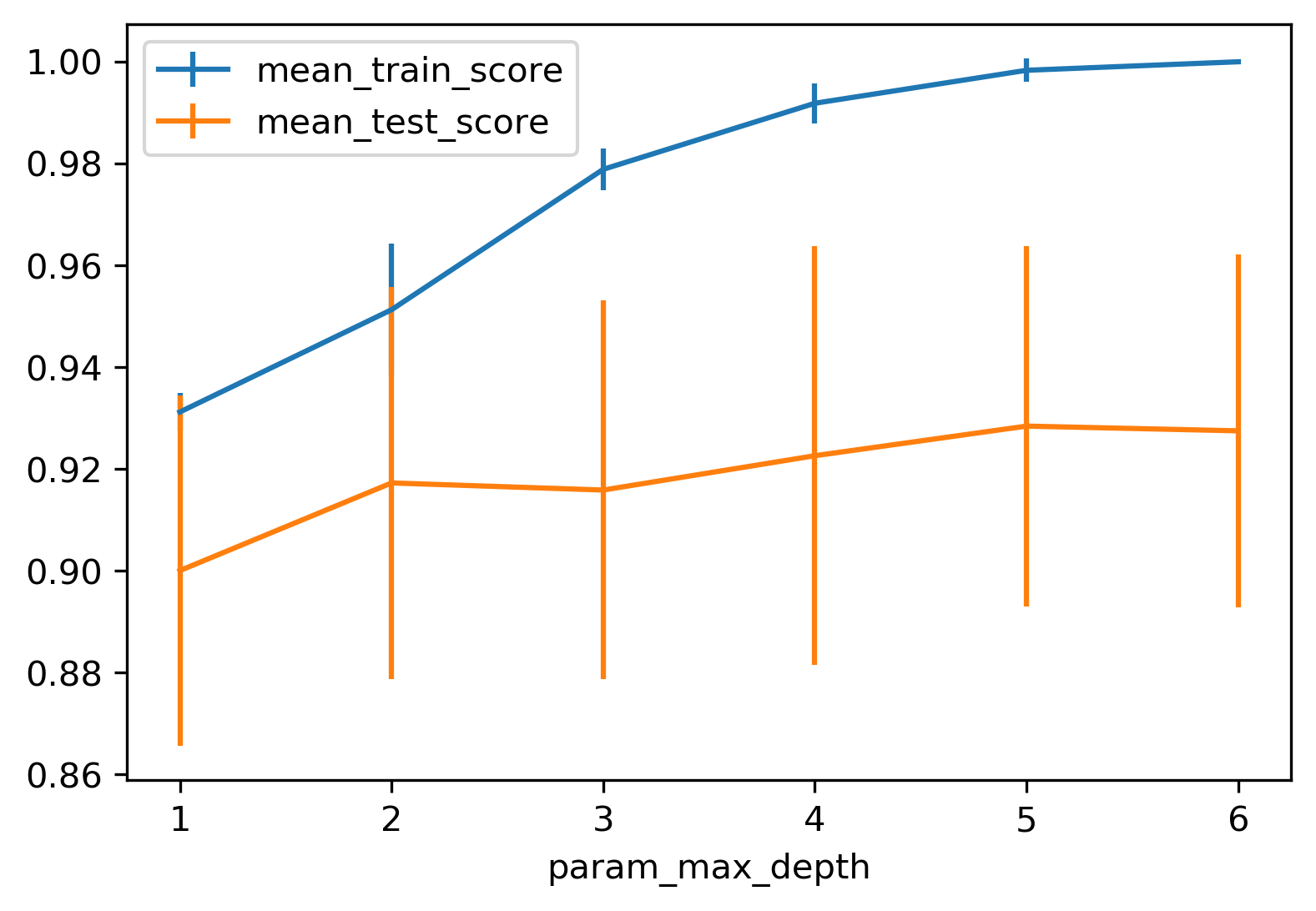
] .center[ :scale 70% ]

So for example, if you want to tune max depth and restricted the depth of the tree. So run a grid search over max depth and you can do the parameter curves as we did before and you can see that maybe depth of five is good on this dataset.

Again, you can see the typical curve with the more complexity you allow in your classifier, the better you get the training set, but possibly you overfit on a test set. So, here, you could say maybe it’s overfitting a little bit, but it’s not very visible.

.smaller[

from sklearn.model_selection import GridSearchCV
param_grid = {'max_leaf_nodes':range(2, 20)}
grid = GridSearchCV(DecisionTreeClassifier(random_state=0),
                    param_grid=param_grid, cv=10)
grid.fit(X_train, y_train)

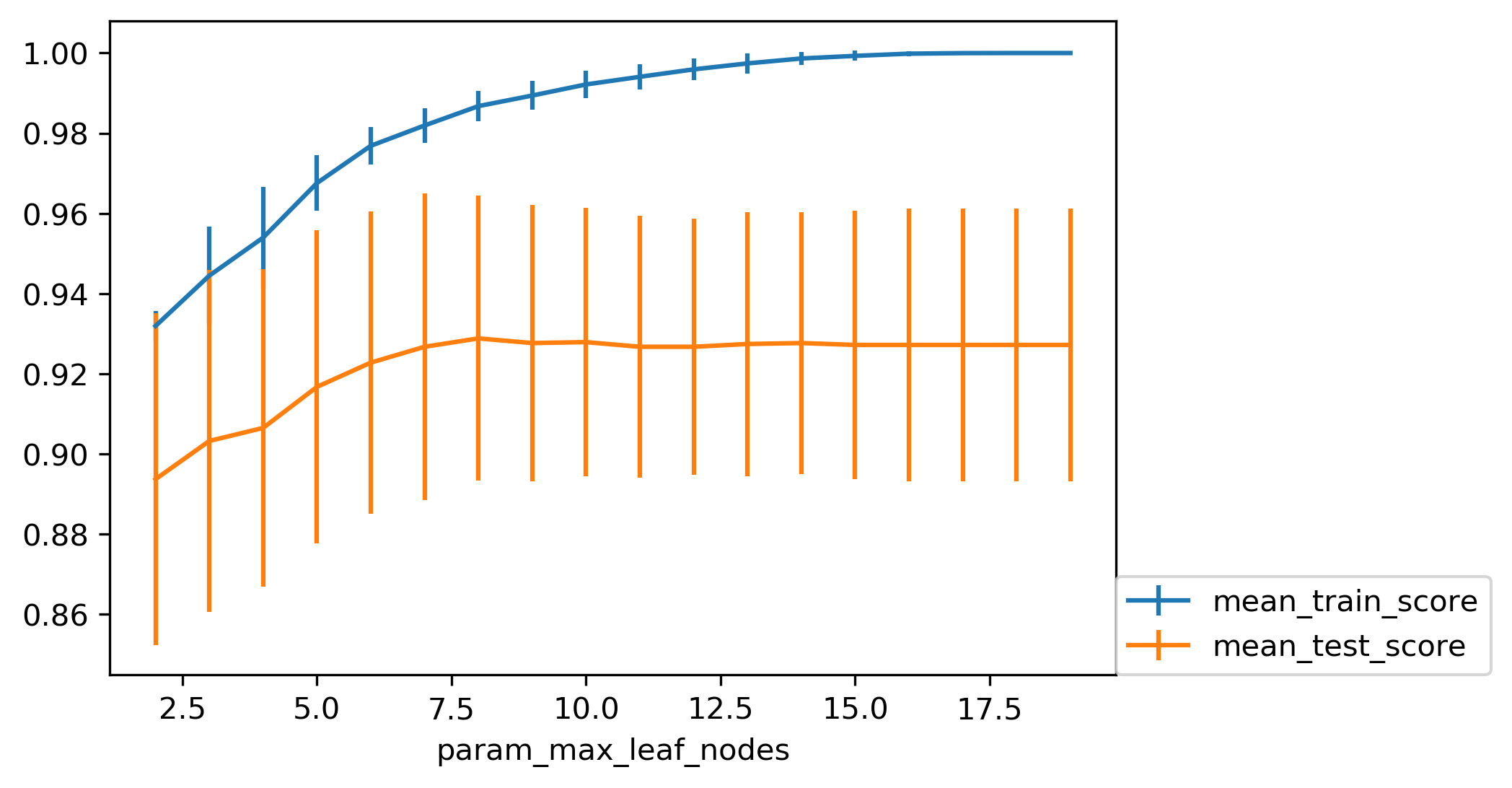
] .center[ :scale 70% ]

Here is if you tune a maximum number of leaf nodes, you can see it’s slightly more overfitting happening but generally, there’s not a big difference on this toy dataset between building the full tree or having a smaller tree. Obviously, if you have a small tree, predictions are going to be faster and need less memory to store and you can explain it better.

So the thing with being able to explain is, if you have a tree up depth 14, then it’s not really explainable anymore, no human can look at all of this and say “Oh, I understand exactly what’s going on”. If you have 8 leaves, it’s a very good chance you can draw this, and you can think about it, and you can understand that.

I wouldn’t really say trees are interpretable but small trees are interpretable. So that’s also the reason why you might want to restrict the rows of the tree. So you can easily communicate and easily explained.

Cost Complexity Pruning¶

.padding-top[ .larger[ $$ R_\alpha(T) = R(T) + \alpha|T| $$ ] ]

$R(T)$ is total leaf impurity

$|T|$ is number of leaf nodes

$\alpha$ is free parameter.

.smaller[

from sklearn.model_selection import GridSearchCV
param_grid = {'ccp_alpha': np.linspace(0., 0.03, 20)}
grid = GridSearchCV(DecisionTreeClassifier(random_state=0),
                    param_grid=param_grid, cv=10)
grid.fit(X_train, y_train)

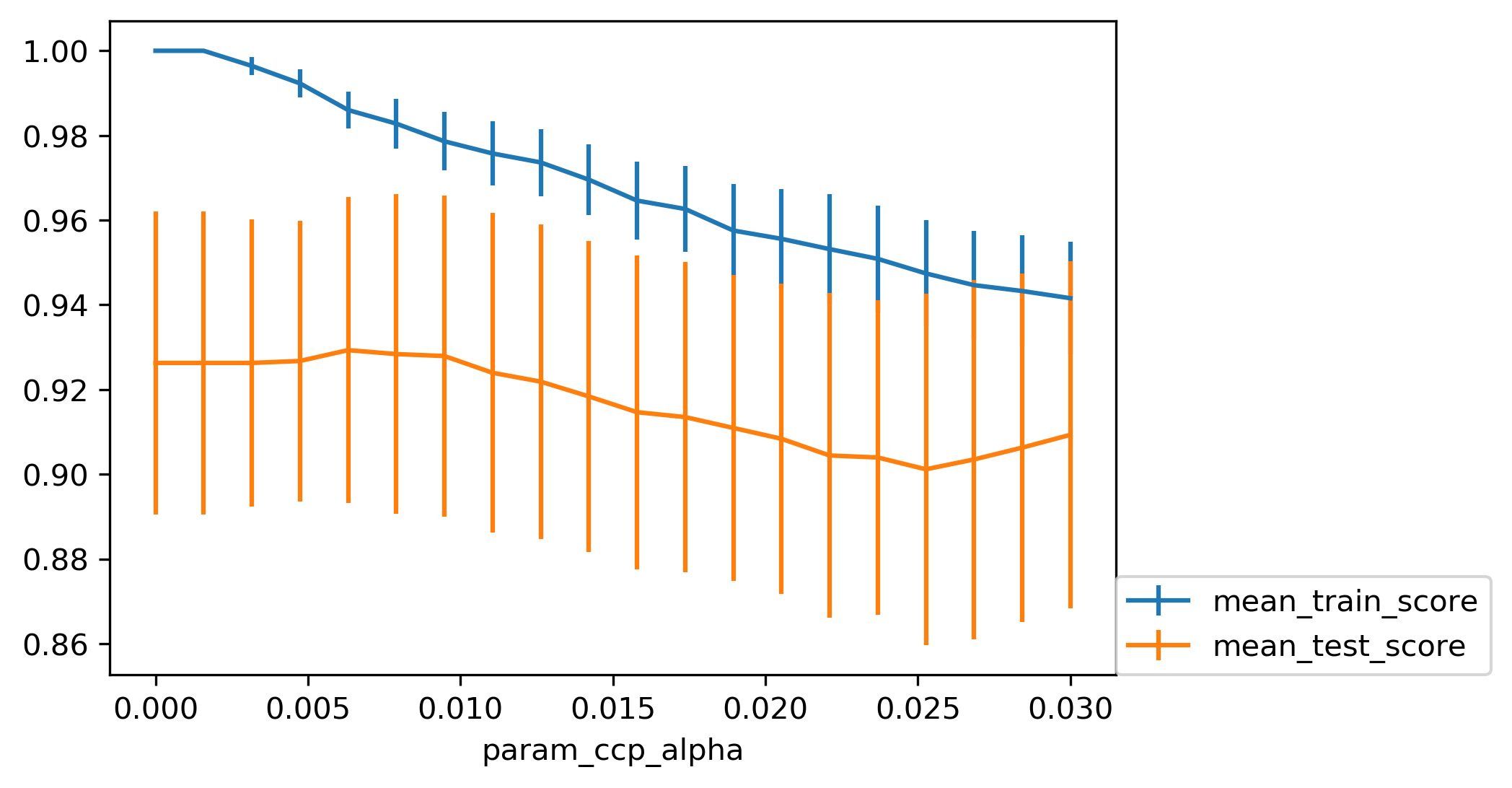] .center[ :scale 70% ]

Efficient pruning¶

clf = DecisionTreeClassifier(random_state=0)
path = clf.cost_complexity_pruning_path(X_train, y_train)
ccp_alphas, impurities = path.ccp_alphas, path.impurities

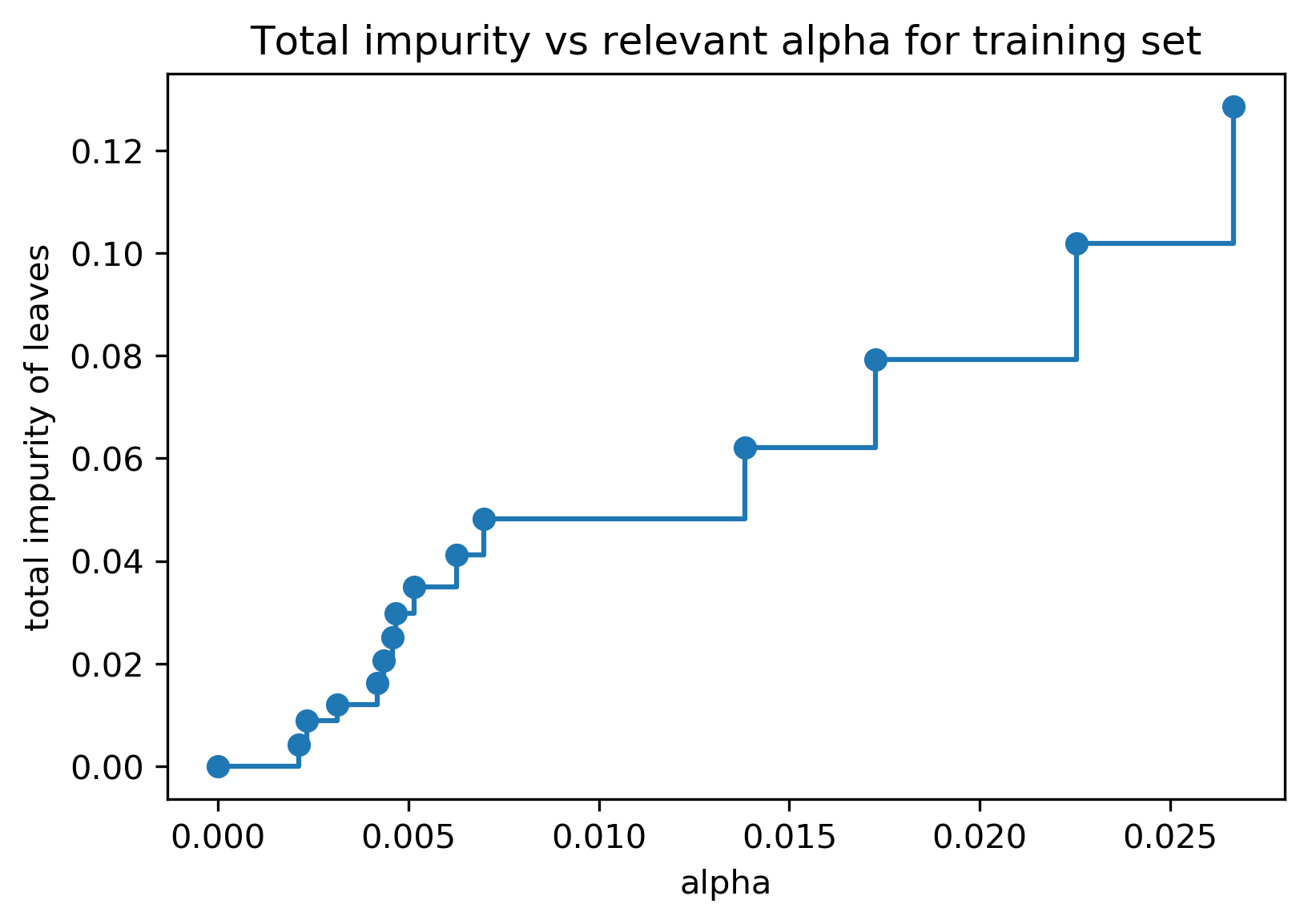.center[ :scale 55% ]

Best post-pruned vs pre-pruned¶

.left-column[

Cost-complexity pruning¶

:scale 70%

] .right-column[

Max leaf nodes search¶

]

#Extrapolation .center[ ]

Trees are actually quite similar to nearest neighbors in some sense because both nearest neighbors and trees pick the average of their neighbors or delete the neighbors’ votes (depending on classification or regression)

In KNearest Neighbors or epsilon nearest neighbors, where you have a radius around the data point in which you look for neighbors. In trees, you look at the same leaf, and you basically let the other point in the leaf vote what the output should be.

Trees are consistent if you give them enough data and they will eventually learn anything because eventually, they’re just like nearest neighbors. Nearest neighbors are very slow to predict because you need to compute the distances to all training points while trees very fast to predict because you just need to traverse the binary tree. One thing that you should keep in mind is that both can’t extrapolate.

#Extrapolation .center[ ]

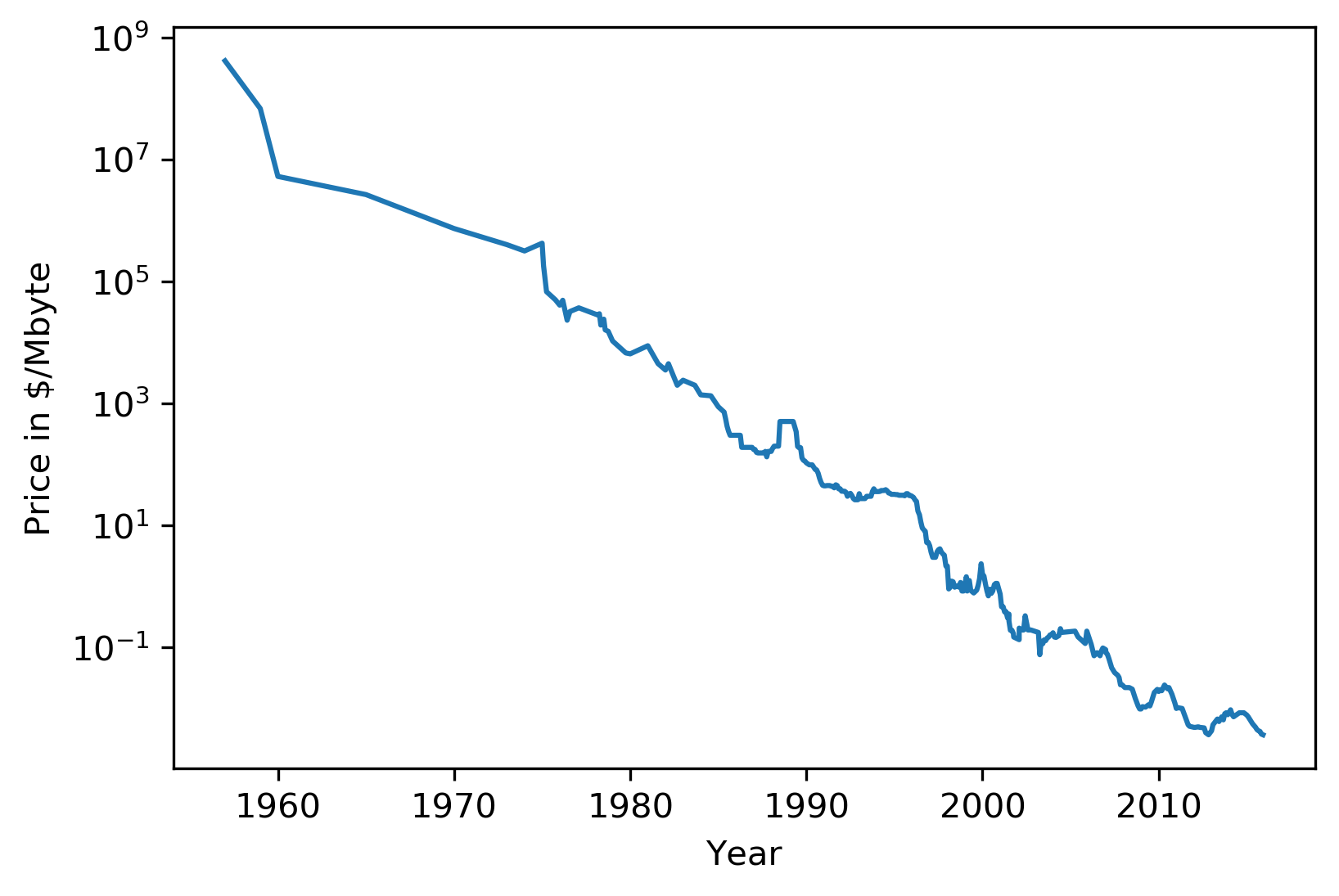
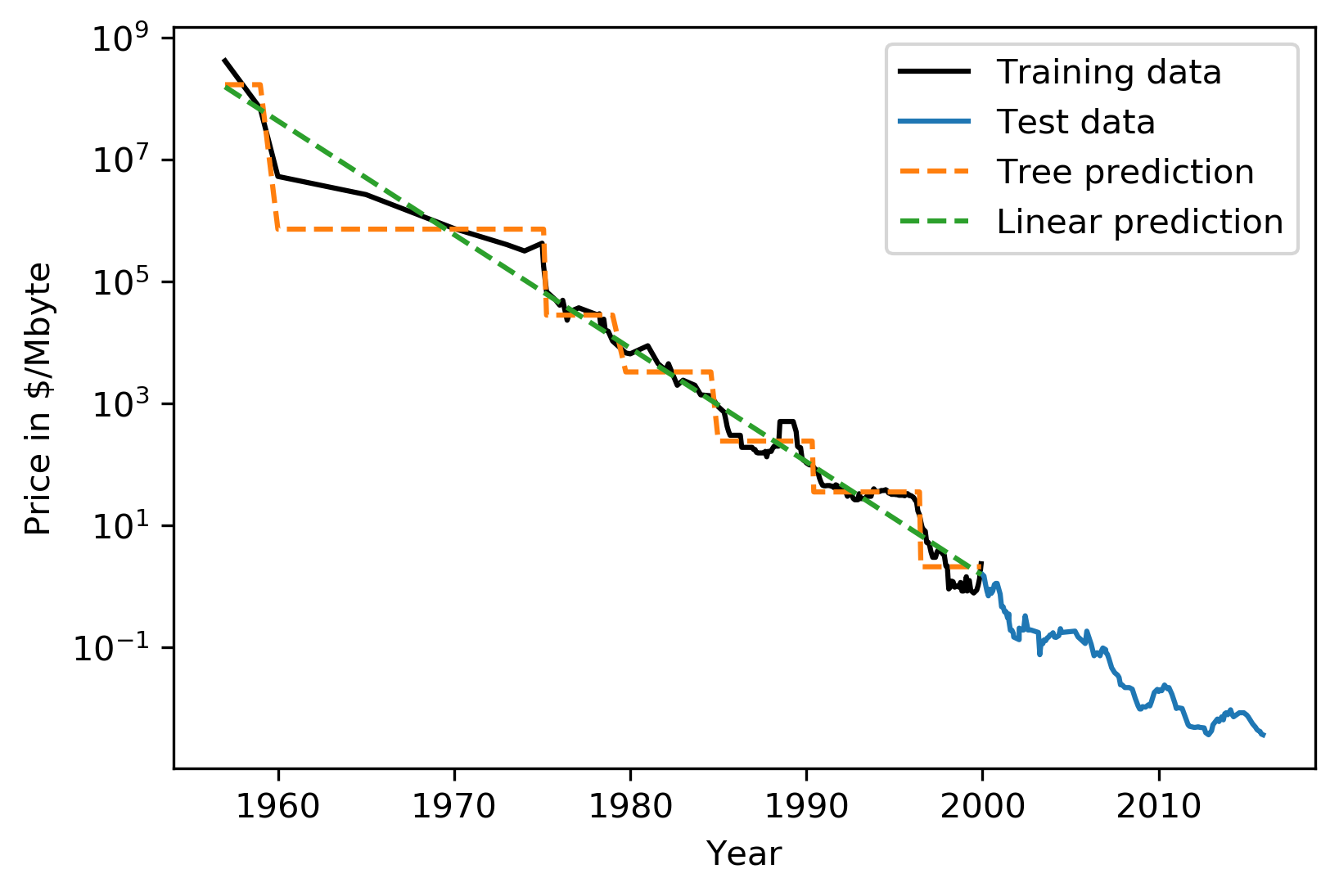
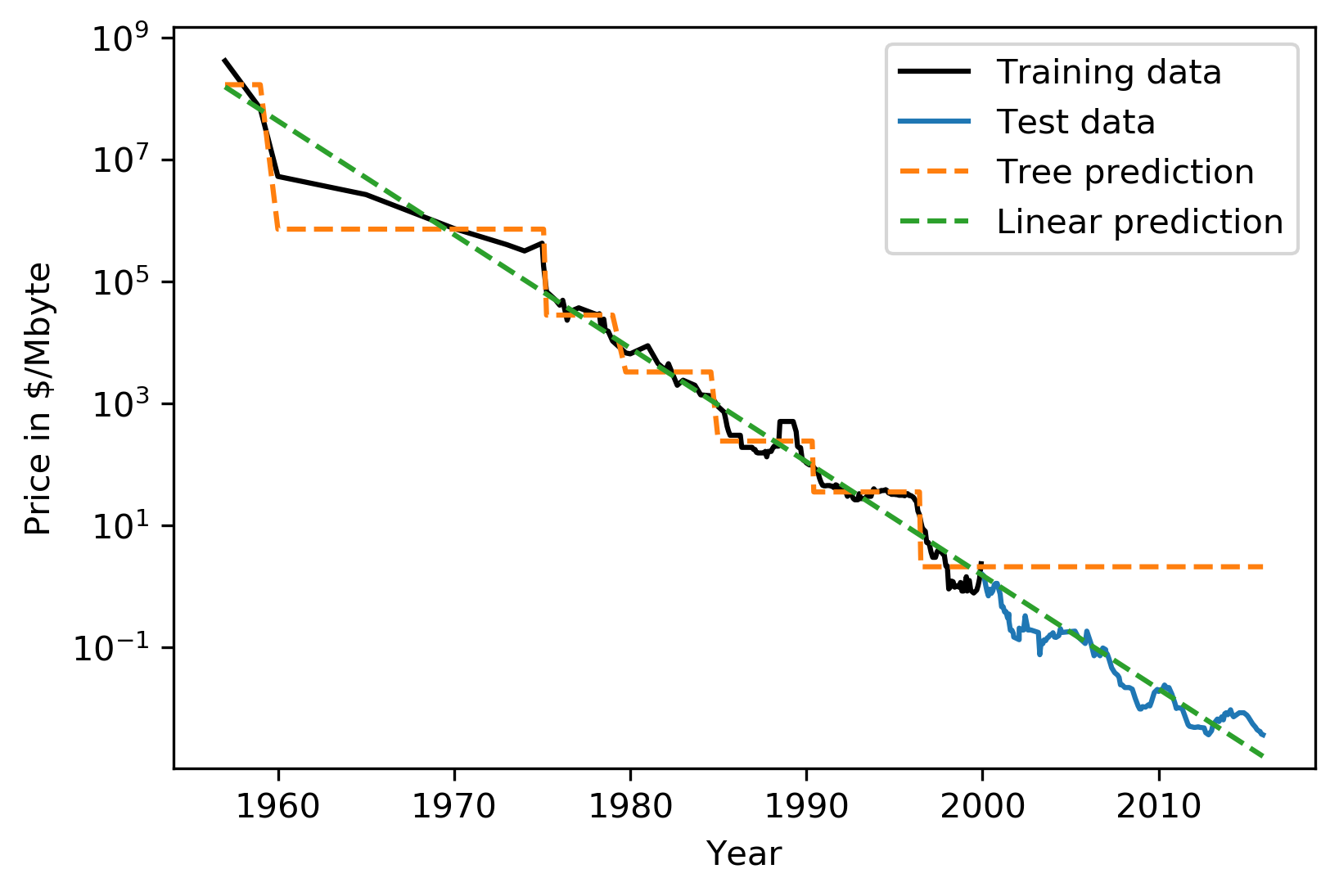
This is the RAM prices in dollar per megabyte historically. This is an instance of Moore’s law. On log scale, it’s pretty linear because of the ram prices half every 18 months or something.

Let’s say I want to build the prediction model for this. And I want to build it up to 2000, and I want to make predictions about the future. Now I’m going to compare a linear model in a tree-based model.

The linear model, I kind of cheated a little bit because I did the log transform so that linear model can actually model it. I didn’t restrict the tree model so it’ll basically learn the training data set perfectly.

Now the question is, if I want to do prediction, what are we going to predict? You probably are not going to be surprised by the linear prediction but you might be by the tree prediction.

The tree predicts just a constant and the constant is basically the last point observed. This is the same thing that the nearest neighbor base model would do. So if you want to predict here, basically, you traverse the tree and you find basically the closest data point to it, the one or the other data point that is in the same leaf, and the ones that will share the leaf with are the ones on the very right. And then it will computer mean of these data points. And the mean is going to be just the value if the leaf is pure. If I did like coarser split level, it will tune the mean of all of these, but it’ll always compute the mean of some data points on the training set. So it’ll never be able to predict these values that are not seen in a training set.

In practice, this is usually not really a big issue. For example, if you want to do like extrapolation like this, you could instead of trying to predict the value, you could use the tree to predict the difference to the last day or to the last year or something like this, and then it would work. But it’s definitely something you should keep in mind. Basically, outside of where you’ve observed training data, it’ll just be a constant prediction. Basically falling back to what it was last seen. That might be a little bit surprising sometimes. Generally, extrapolation in machine learning is hard. And if you need to extrapolate, there’s a chance you’re not going to be able to do with any model. But in particular, for tree-based and nearest neighbor based models, you should keep in mind that they can’t do that.

Relation to Nearest Neighbors¶

Predict average of neighbors – either by k, by epsilon ball or by leaf.
Trees are much faster to predict.
Both can’t extrapolate

FIXME plots

Instability¶

.left-column[ .tiny-code[

X_train, X_test, y_train, y_test = train_test_split(
    iris.data, iris.target, stratify=iris.target, random_state=0)
tree = DecisionTreeClassifier(max_leaf_nodes=6)
tree.fit(X_train, y_train)

] :scale 70% ] .right-column[ .tiny-code[```python X_train, X_test, y_train, y_test = train_test_split( iris.data, iris.target, stratify=iris.target, random_state=1) tree = DecisionTreeClassifier(max_leaf_nodes=6) tree.fit(X_train, y_train)

]
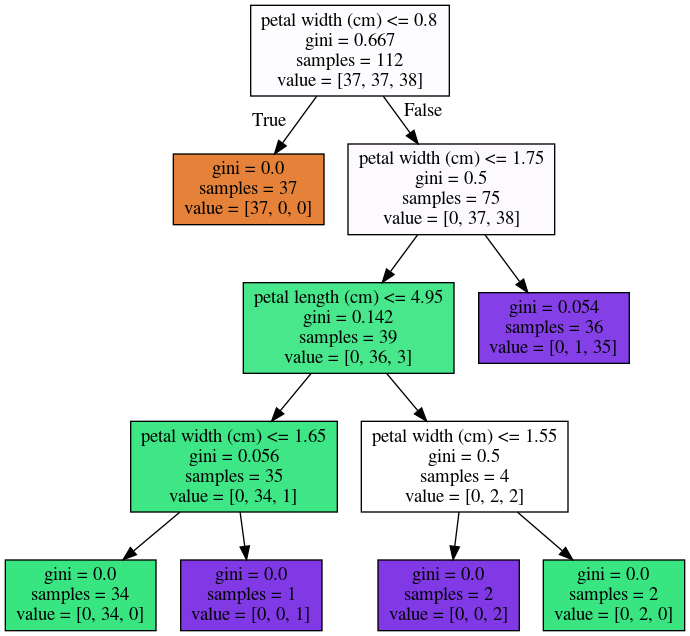
.center[![:scale 70%](images/instability_2.png)
]]


Another weakness of trees that I want to mention is that
they are very unstable. Using the iris dataset, let's say I
want a small tree. So I say I want a maximum of six leaves
nodes and I split my Iris dataset, and I build the tree, and
then I split the same data set again, and take a different
random state. Hopefully, I would assume that if it's the
same dataset, and I split randomly, then the models should
be similar. However, if you look at these models, even in
the root note, the very first decision it made is different.
One compares petal length to 2.45 while the other compares
pedal width to 0.8.

And the number of points that are split off are different
too. So there's not really an easy correspondence between
these two trees. So this is sort of a caveat about
interoperability. You can interpret the tree but maybe if
the dataset was only slightly different, the tree might look
completely different. So this tree structure is really
something that's very unstable.

+++

## Feature importance

.left-column[
.tiny-code[```python
X_train, X_test, y_train, y_test = train_test_split(
    iris.data, iris.target, stratify=iris.target, random_state=0)
tree = DecisionTreeClassifier(max_leaf_nodes=6)
tree.fit(X_train,y_train)
```]
.center[![:scale 60%](images/instability_1.png)
]
]

.right-column[

.tiny-code[
```python
tree.feature_importances_
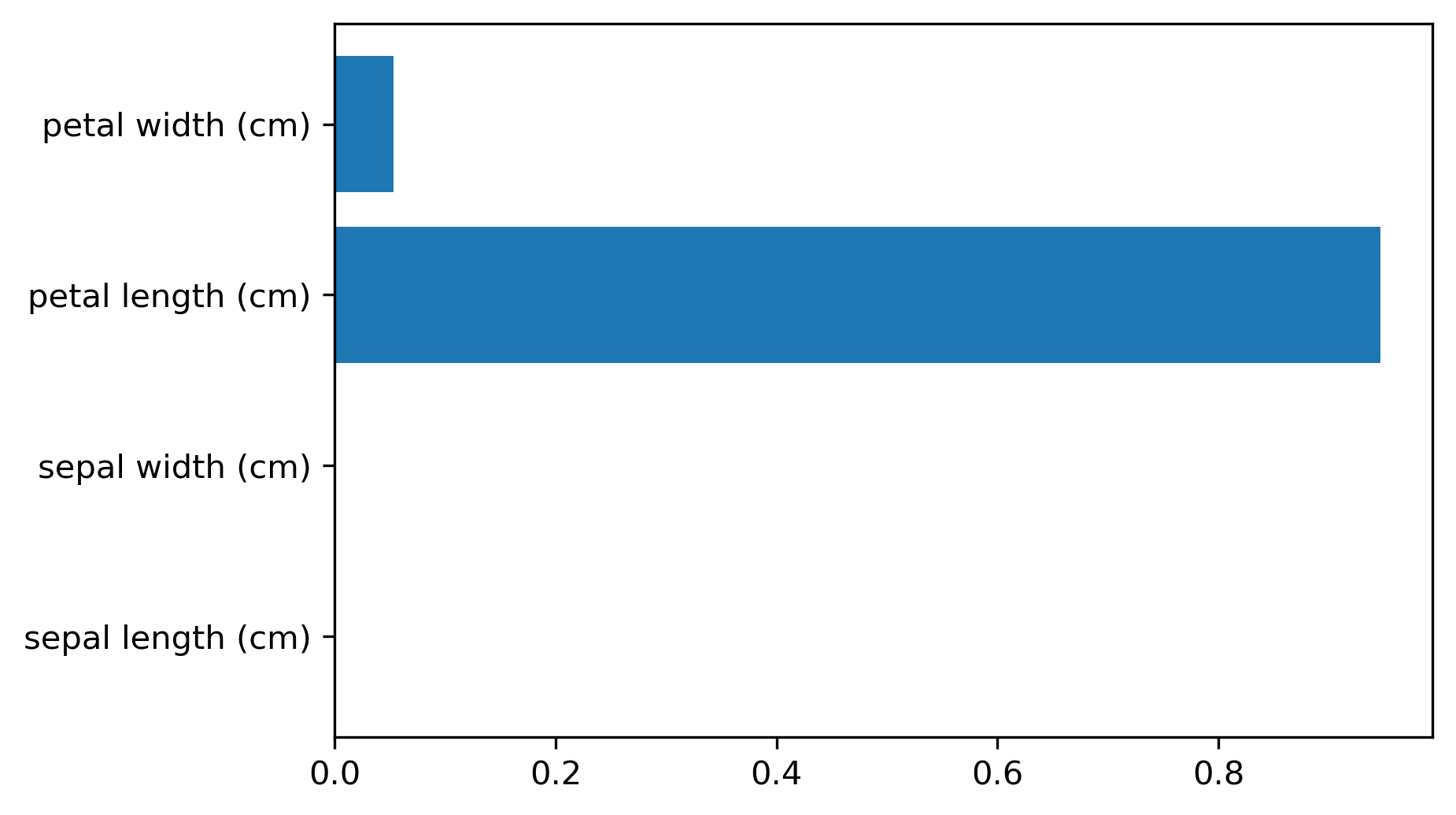
array([0.0, 0.0, 0.414, 0.586])

]

:scale 80%

]

Another interesting feature of trees that I want to mention is feature importance. While looking at the trees, a nice way to inspect the tree if it’s small, if your trees very big, it’s very hard to understand what’s happening in the tree. So what you can get out is how important each feature is for the tree. This is similar to the coefficients in the linear model, where you can see that “this feature influences the model in this way”. And the way this is done is basically each time a particular feature was chosen in a tree, you accumulate how much it decreased the impurity. It’ll give more importance to features that were used often and where to use of it, than decreased impurity.

Problem with the importance is you have the same issues with instability. Because the tree structures unstable, the features picked is unstable and so the importance will be unstable.

Similar to L1 norm, if you have too many correlated features, it might pick one or the other. If you have very correlated features, basically, the feature importance could be anything. Any linear combination of the two is completely equivalent. So keep that in mind when looking at feature importance. But they’re a very nice way to summarize what the tree does if you’re in reasonably low dimensions and your tree is big. Obviously, if you’re in super high dimensions, you might not be able to look at them, you might be able to look at the most important features.

The question was if use a feature multiple times, do I add up the degrees in purities and the answer is yes.

Question is can I explain the difference between extrapolating and generalizing. In generalizing, usually you make this IID assumption that you draw data from the same distribution, and you have some samples from the distribution from which you learn, and other samples from a distribution which you want to predict. And if you’re able to predict well, then it is generalizing.

Here in the extrapolation example, the distribution that I want to try to predict on was actually different from the distribution I learned on because they’re completely disjoint. The years I trained on and the years that I’m testing on are completely disjoint and the target range is also completely disjoint. So this is not an IID task.

In particular, even if it was IID, extrapolation sort of means looking at things outside the training set.

One more comment about feature importance is that they give you the importance of a feature, but not the direction. If you look at the linear model and you say that a coefficient is large, or a coefficient is very small, this means for regression, if it’s larger than it has a positive influence on target, or if it’s classification, this feature has a positive influence to being a member of this class. For trees, you don’t have the directionality, here you only get this is important only to make a decision. And the relationship with the class might not be monotonous.

So you only have a magnitude you don’t have a direction in the importance.

Unstable Tree $\rightarrow$ Unstable feature importances.
Might take one or multiple from a group of correlated features.

Categorical Data¶

Can split on categorical data directly
Intuitive way to split: split in two subsets
2 ^ n_values many possibilities
Possible to do in O(n_values . log(n_values)) exactly for gini index and binary classification.
Heuristics done in practice for multi-class.
Not in sklearn yet

You can use categorical data in trees, and you can do this in R up to a couple of hundred different values. In scikit-learns, unfortunately, it’s not there yet.

The cool thing about it working with categorical data is that it allows you to split into any subsets of the categories. So if you have, let’s say have one categorical variable with five levels, or five different values, you could split it in a tree in all possible ways. So in three, two, four, one and with all of the possible combinations.

Usually, if you would want to do that you will need to try out two to the power number of values many possibilities for the splits, two to the power five in this example. That might not be feasible. But actually, for some criteria, for example, for Gini index you can do this efficiently in linear time.

So in scikit-learn right now, you have to use one hot encoding, which is not powerful because one hot encoding can only split one feature at a time. So you would need to grow a much deeper tree to split categorical variable in all possible ways.

There’s also I think in R there’s a bunch of tree implementations that work with missing values and there are several different strategies to deal with missing values.

But it’s also not entirely clear which strategy to deal with a missing value in trees is the best. So one strategy is, if you have a missing value, you can basically go down both sides at once, if the question is about the value that’s missing, just go down both things. But that’s kind of slow. The other thing that it’s actually just another value you can split on and you can say, “if I split on a missing value, I have a separate branch just for missing values.”

But you can easily emulate this by replacing it with a binary feature which says missing or not missing.

Predicting probabilities¶

Fraction of class in leaf.
Without pruning: Always 100% certain!
Even with pruning might be too certain.

You can also predict probabilities with trees. Although, I would recommend against it. The issue with trees is that they are very good at overfitting, they can fit anything if I grow them deep enough. If I grow them to the full depth, they will always be 100% certain. Because the probability is the fraction of the number of points in the leaves that belong to this class. So if I have a leaf with like 10 data points, and 7 of them belong to class A, then it will say, with 70% probability a point here is class A. But if you split until everything’s pure, it will always be 100% certain, which is pretty meaningless.

So you can do some pruning, and you can restrict the rows of the tree, but it still might be certain, and so the probability estimates that come out of a tree might not be very good.

FIXME PLOT

Conditional Inference Trees¶

Select “best” split with correcting for multiple-hypothesis testing.
More “fair” to categorical variables.
Only in R so far (party)

Different splitting methods¶

.center[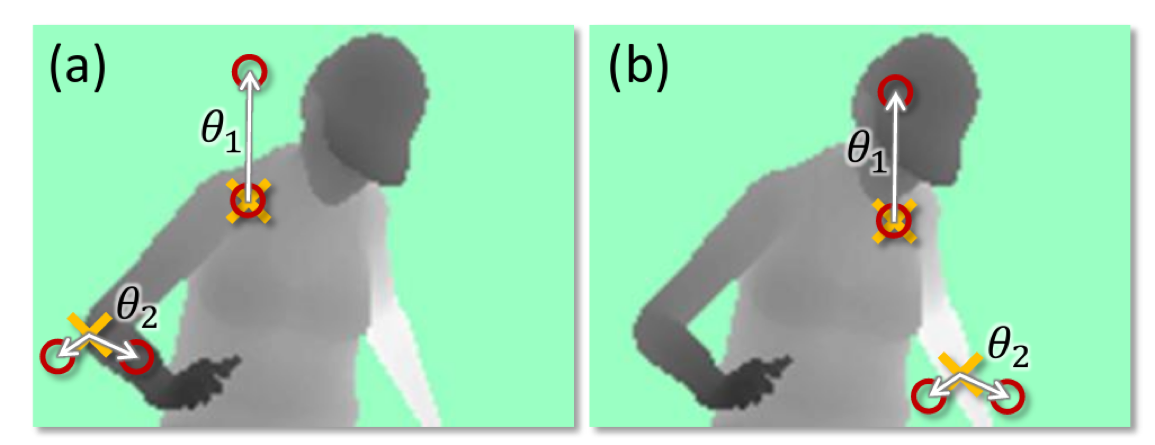 :scale 80% ]

.smaller[(taken from Shotton et. al. Real-Time Human Pose Recognition ..)]

Another reason why trees are very popular is since they’re very flexible. This is actually from a paper about the Kinect version one. Which allows you to use your body as a game controller and builds like a 3d image of you and follows your hand. They used decision trees in a quite clever way to find where different parts of the body are.

Here you have a depth image of a person. The questions that are asked are not looking at single pixels but if you want to decide for a particular pixel, you can ask questions about pixels that are somewhere else. So you can ask, how deep is the pixel five above me? How deep is the pixel five below me? And so on. And it can also do comparisons in saying, what’s the difference between the value here and there? And so basically, you can come up with more complex ways to ask questions. And this leads to more powerful tree models. That’s quite common in computer vision to ask either about comparing pixels or comparing regions of pixels or something like that.

Usually, by default, you just threshold each feature but you can come up with arbitrary things. I also know models where each node is like….linear model, for example, and the test is what the response of the linear model is?

Shortcomings of the trees are they very unstable, they can’t extrapolate and they tend to overfit a lot.

Could use anything as split candidate!
Linear models used if extrapolation is needed.
Computer vision: pixel comparisons
Kinect (first generation): depth comparison

import numpy as np
import matplotlib.pyplot as plt
import sklearn
sklearn.set_config(print_changed_only=True)
import pandas as pd
from sklearn.model_selection import train_test_split
from sklearn.pipeline import make_pipeline
from sklearn.preprocessing import scale, StandardScaler

from sklearn.datasets import load_breast_cancer
cancer = load_breast_cancer()

print(cancer.DESCR)

X_train, X_test, y_train, y_test = train_test_split(
    cancer.data, cancer.target, stratify=cancer.target, random_state=0)

Applied Machine Learning in Python

Decision Trees¶

Trees, Forests & Ensembles¶

Why Trees?¶

Decision Trees for Classification¶

Idea: series of binary questions¶

Building Trees¶

Criteria (for classification)¶

Prediction¶

Regression trees¶

Visualizing trees with sklearn¶

Visualizing trees with sklearn¶

Parameter Tuning¶

No pruning¶

max_depth = 4¶

max_leaf_nodes = 8¶

min_samples_split = 50¶

Cost Complexity Pruning¶

Efficient pruning¶

Best post-pruned vs pre-pruned¶

Cost-complexity pruning¶

Max leaf nodes search¶

Relation to Nearest Neighbors¶

Instability¶

Categorical Data¶

Predicting probabilities¶

Conditional Inference Trees¶

Different splitting methods¶

tree visualization¶

Parameter Tuning¶

Exercise¶