import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
import sklearn
sklearn.set_config(print_changed_only=True)
(Stochastic) Gradient Descent, Gradient Boosting¶
02/19/20
Andreas C. Müller
We’ll continue tree-based models, talking about boosting. Finally, a technique called calibration that looks somewhat similar to ensembles but has the goal of obtaining good probability estimates from any classifier.
FIXME regularization parameter mentioned before introduced FIXME explain regularization better FIXME parameter tuning example FIXME symmetric trees FIXME actually write out gradients maybe
FIXME: add example of calibrated and inaccurate vs accurate but not calibrated! (always saying 50% is calibrated) FIXME: brier score decomposition FIXME calibration scores FIXME maybe saying “sort” before binning is confusing? FIXME move calibration after metrics?
Partial dependence plot. how is that different from feature importances. calibration curve plotting: bins are different for hist and calibration curve? slide 27: maybe put probabilities on x axis? calibration curve: blue histogram is number of total points, y axis not labeled
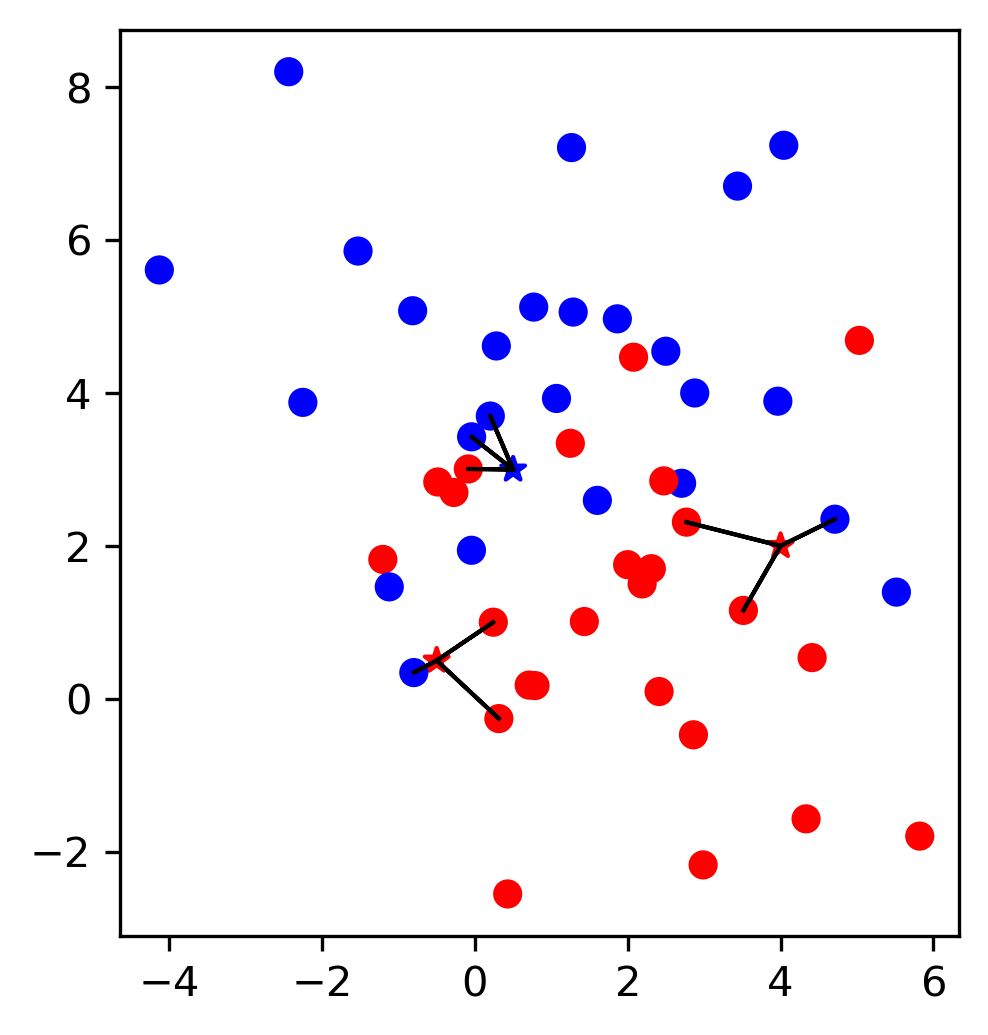
Reminder: Gradient Descent¶
.right-column[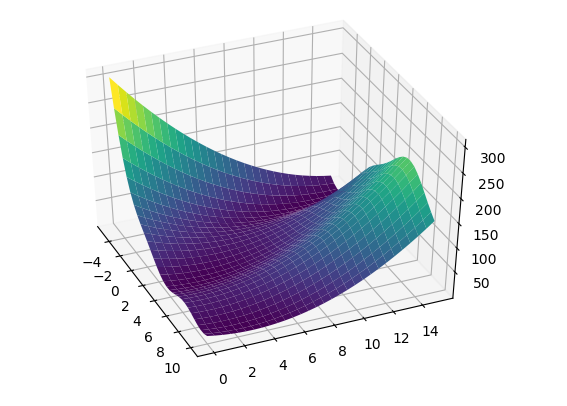 ]
]
Want: \($\arg \min_w F(w)\)$
Initialize \(w_0\)
Converges to local minimum
First, let’s talk about Gradient Descent. So we have some function we want to minimize here the function is Lasso training data set plus the regularizer. F is the objective of the model and I want to find the best parameter setting w. The way gradient descent works are that we initialize it with some W and then we compute a gradient then we walk down the gradient by a small step. This converges to a local minimum in the function. For linear models, there’s only one global minimum. Basically, any optimization algorithm you can think of will always converge to the same solution, they only converge at different speeds.
Reminder: Gradient Descent¶
.center[
 ]
]
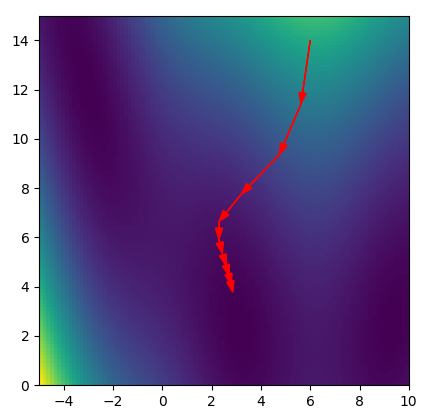
Pick a learning rate¶
.center[
 ]
]
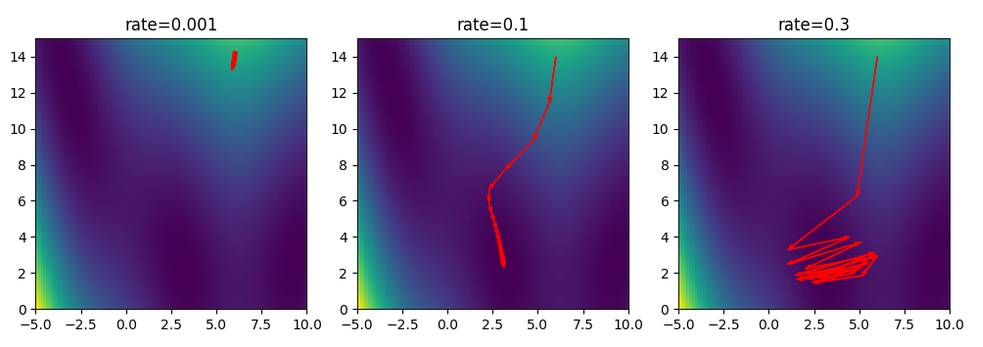
A little bit of an issue here is picking a learning rate which is how big a step are you making. If you make too small a step, then you’re going to get stuck wherever you’re started. If you pick the right step size, you can make very quick progress. If you pick too a big step size, you’re going to be missing the target and just jumping around the target. This is a very simple optimizer. But it’s not great and it’s not very fast because you need to compute gradients over the whole dataset. What you can do instead is you can approximate a gradient by looking only a single data point at a time.
(Stochastic) Gradient Descent¶
.smaller[ Logistic Regression Objective:
Gradient:
Stochastic Gradient: Pick \(x_i\) randomly, then
In practice: just iterate over i. ]
Looking at the Logistic Regression, the functional Logistic Regression we want to minimize is the log loss plus the regularizer. Instead of looking at the gradient for the whole sum here, we can get a stochastic approximation of the gradient by looking at only one of the sums at a time. In practice, we iterate over the dataset and go one by one through all the data points. We make sure we shuffle them before. Then we do small gradient steps. This is a very bad optimizer compared to the SAG but it can go very quickly over a lot of data.
SGDClassifier, SGDRegressor and partial_fit¶
## Run until convergence
sgd = SGDClassifier().fit(X_train, y_train)
## Run one iteration over a batched dataset
sgd = SGDClassifier()
for X_batch, y_batch in batches:
sgd.partial_fit(X_batch, y_batch, classes=[0, 1, 2])
## Run several iterations over a batched datasets
for i in range(10):
for X_batch, y_batch in batches:
sgd.partial_fit(X_batch, y_batch, classes=[0, 1, 2])
Fit works just like everywhere else. Partial fit you can call it with different batches of data and this will keep fitting the model. One thing that you should keep in mind for the classifier is that you need to give it the classes at the beginning because it doesn’t know how many classes there are and at the first time, not all the classes might be present in the data you give it to. So you need to specify how many classes there are. Partial fit doesn’t do loops over a dataset. So if you want to use a partial fit, and you want to loop over dataset multiple times, you have to set the loop yourself. If you loop over a dataset, if you do more of gradient descent, then you get better results. This code is the same code for all combinations of losses and regularizers because it’s very simple to write this down.
SGD and partial_fit¶
SGDClassifier(), SGDRegressor() fast on very large datasets
Tuning learning rate and schedule can be tricky.
partial_fit allows working with out-of-memory data!
This is implemented in SGD classifier, and SGD regressor and you can use it in very large data sets. It’s a little bit tricky to tune the learning rate and so you can either pick as constant learning rate, or you can pick an exponentially decreasing learning rate. There’s one that’s called optimal. If you scale your data to standard division 1, then the optimal one will often work well but it’s not actually optimal on any sense. This will allow you to give you something quickly on a big data set. There’s also another thing you can do, there’s a method called partial_fit that these models have which allows you to iteratively fit feed it data. If you have like streaming data coming in and you having infinite data, you can just keep giving it more and more data called partial_fit. This method will update the model. In scikit-learn, if you call fit multiple times it will always forget whatever it saw before. Each fit resets the model while partial fit will remember what it saw before and keeps fitting the model. SGDClassifier() and SGDRegressor both have a whole bunch of different loss function penalties so they both can do elastic net penalty and the classifier can do logistic loss and hinge loss and squared hinge loss and the regressor can do Huber loss and squared error and absolute error. So there are many, many different choices for different loss functions.
Boosting¶
.larger[ \($f(x) = \sum_k g_k(x)\)$
Family of algorithms to create “strong” learner \(f\) from “weak” learners \(g_k\).
AdaBoost, GentleBoost, LogitBoost, … ]
Trees or stumps work best
Gradient Boosting often the best of the bunch
Many specialized algorithms (ranking etc)
This is an instance of a more general family of models, called boosting models, which all iteratively try to improve a model built up from weak learners. Gradient boosting is this particular technique where we are trying to fit the residuals, and it’s been found to work very well in practice, in particular if you’re using shallow trees as the weak learners. In principle, you could use any model as a weak learner, but trees just work really well.
Gradient Boosting¶
Gradient boosting is one of the most successfull supervised machine learning methods in practice. It’s often used in kaggle to win competition, it’s used for credit scoring, it’s one of the standard tools of the trade. It’s one of the best of-the-shelf models A standard implementation that people use is XGBoost, but there’s also an implementation in scikit-learn, and we’ll talk about both of them.
Last time we talked about Random forests, which builds many trees independently, each randomized in a different way, and then averages their predictions. Gradient boosting on the other hand builds trees one by one in a sequential manner, with each tree requiring the results of previous trees. Often, Gradient boosting is done with very small trees, or even decision stumps, which is trees of depth one, so a single split.
Gradient Boosting Algorithm¶
–
\(y \approx\) 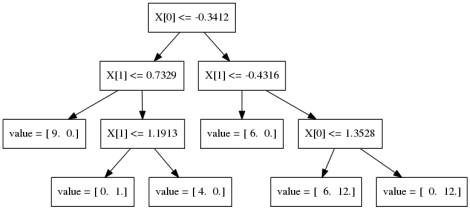 +
+ 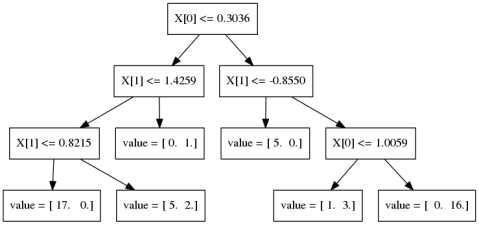 +
+ 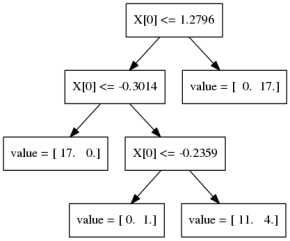 + …
+ …
Let’s look at the regression case first. We start by building a single tree f1 to try to predict the output y. But we strongly restrict f1, so it will be rather bad at predicting y. Next, we’ll look at the residual of this first model, so y - f1(x). We now train a new model f2 to try and predict this residual, in other words to correct the mistakes made by f1. Again, this will be a very simple model, so it will still not be able to fix all errors. Then, we look at the residual of both of the models together, so y
f1(x) - f2(x), so the mistakes that could not be fixed by f2, and we build f3 to fix that, and so on. This is natural for regression. For classification this is not as clear. For binary classification you use log-loss, or rather you apply the logistic function to get a binary prediction, for multi-class you can use 1 vs rest.
So we’re sequentially building up a model using what’s called “weak learners”, small trees, and create a more powerful composite model.
Gradient Boosting Algorithm¶
\(y \approx \gamma\)  + \(\gamma\)
+ \(\gamma\)  + \(\gamma\)
+ \(\gamma\)  + …
+ …
Learning rate \(\gamma, i.e. 0.1\)
Iteratively add regression trees to model
Use log loss for classification
Discount update by learning rate
FIXME plot for regression models Come back to this
Gradient Boosting is Gradient Descent¶
.left-column[
Linear regression¶
optimize:
gradient descent: \($w_{j+1} = w_j - \gamma \frac{\partial L(\mathbf{x}_i, y_i, \mathbf{w}, b)}{\partial\mathbf{w}}\)$ ]¶
.right-column[
Gradient Boosting¶
optimize:
gradient descent: \($\hat{y}_{j+1} = \hat{y}_j - \gamma \frac{\partial L(y_i, \hat{y}_i)}{\partial\hat{y}}\)$ ]
#GradientBoostingRegressor
.center[
 ]
]
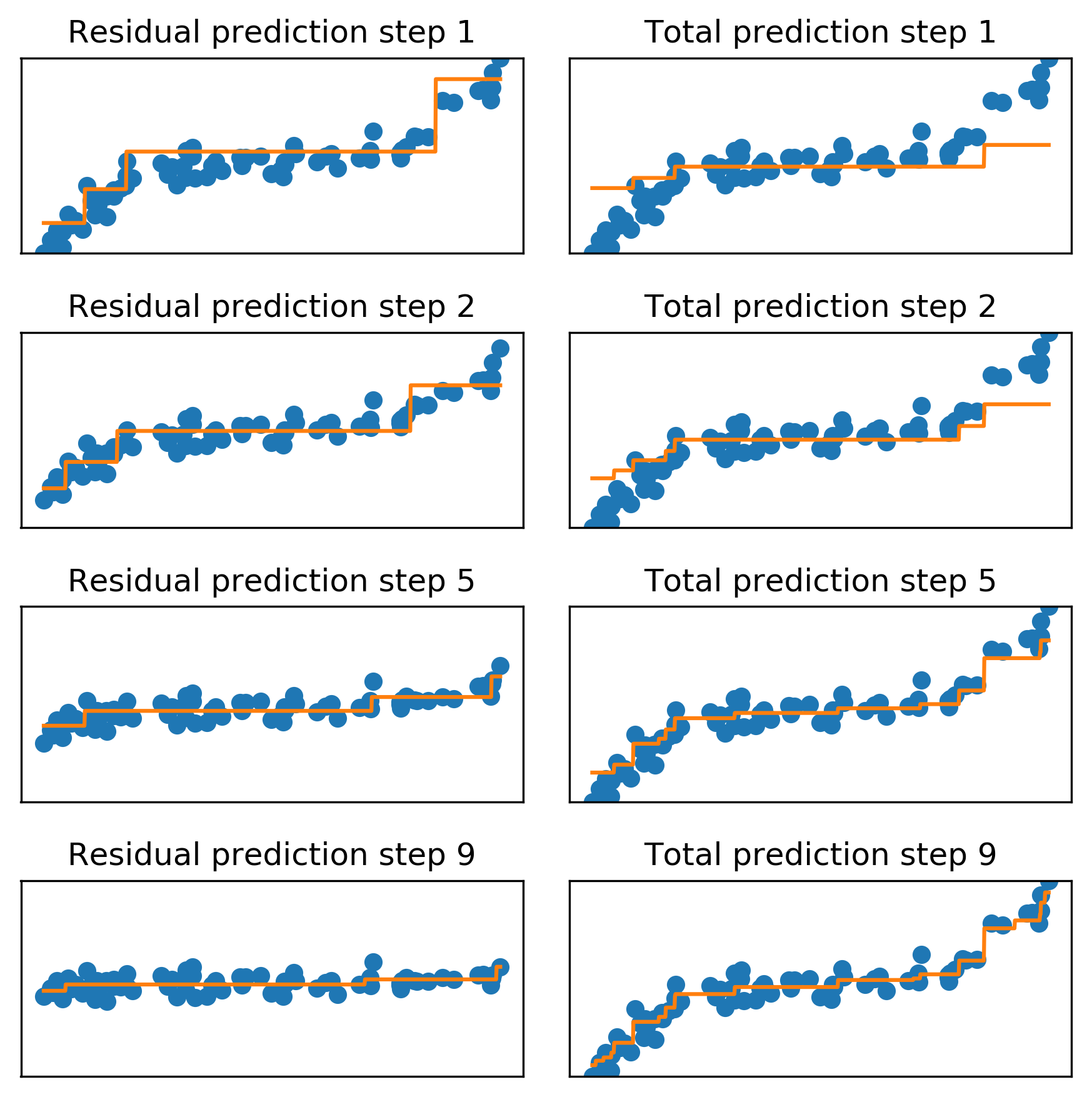
Here’s an illustration for doing this for regression. This is a 1D regression dataset for illustration purposes here to form features on the x-axis, the prediction is on the y-axis.
In the first step, I’m just fitting my tree to the data. I use a simple tree of depth 3. The depth 3 tree is not able to completely model the data and so the orange is the tree that was fit. After this first step, I look at the total predictions. So this is just gamma times the predictions made by the first tree. So you see everything is sort of squashed together. This is the effect of gamma. The blue points here in this next panel is this data minus the minus the predictions from step one, and so this is the residual. It still looks pretty much the same, because we took only a small step. Then I fit another tree to this residuals again of depth three. Then here’s the total prediction, which is gamma times the first tree plus gamma times the second tree, followed against the original data. The orange has more steps now because it’s a combination of two trees.
As I continue the same procedure until step five, you can see that residual gets much smaller and it has learned most of the variations in the data. A total linear combination of all the trees and learning looks like this. And if I keep doing this, then at some point, residuals will become very small. And the total prediction will fit the data better and better.
The question is can I extrapolate?
The answer is no.
The question is how is this different?
And it’s quite different. It’s kind of hard for me to answer his question.
A) The combination of stumps is different than building a deeper tree because you always apply all the splits to the whole dataset. Whereas if you make a tree deeper, you will have different splits on the deeper nodes. If you have already like 10 nodes, and you want to grow one more level, each of these parts of the data will have a different split. Whereas if I add another stump it will be on a global level. In decision trees, decisions are very hard. And here you don’t trust any hard decisions. So you only go a little bit in each direction.
B) This works way better.
So this was for regression and because it’s easier to visualize, you can do the same thing for classification.
Basically, what gradient boosting for classification does is you’re letting regression trees to learn decision function. So basically, you’re doing regression again, but you’re doing logistic regression. Instead of using a linear model for logistic regression, we’re now using this linear combination of trees. So in other words, what we’re doing is we’re applying a log loss, and we’re trying to find the regression function that has a small log loss. This f is the decision function that we’re doing. And so inside a gradient boosting classifier, you’re not actually learning classification trees, you’re learning regression trees, which are trying to predict the probability, which is quite different.
The question is, how they’re different?
The same is true for f1. If I fit f1, exactly to y this becomes 0. One reason is the gamma, which means I only go a small step. But even if I set gamma equal to one, the point is that I restricted my f1 to not completely fit the data. I’m not trying to completely overfit the data, I’m trying to use a simple model. So if I use a tree of depth one, there will be a very large residual.
Gradient boosting for classification¶
Logistic regression:
Gradient boosting: \($\min_{y_i\in \mathbb{R}^n}\sum_{i=1}^n\log(\exp(-y_i \hat{y}_i) + 1)\)$
Multiclass Gradient Boosting¶
Multinomial logistic regression: \($p(y=c|x) = \frac{e^{\textbf{w}_c^T\textbf{x} + b_i}}{\sum_{j=1}^k e^{\textbf{w}_j^T\textbf{x} + b_j}}\)$ Multi-class gradient boosting: \($p(y=c|x) = \frac{e^{\hat{y}^{(c)}}}{\sum_{j=1}^k e^{\hat{y}^{(j)}}}\)$ One regression tree per class (per gradient step).
#GradientBoostingClassifier / HistGradientBoostingClassifier
.center[
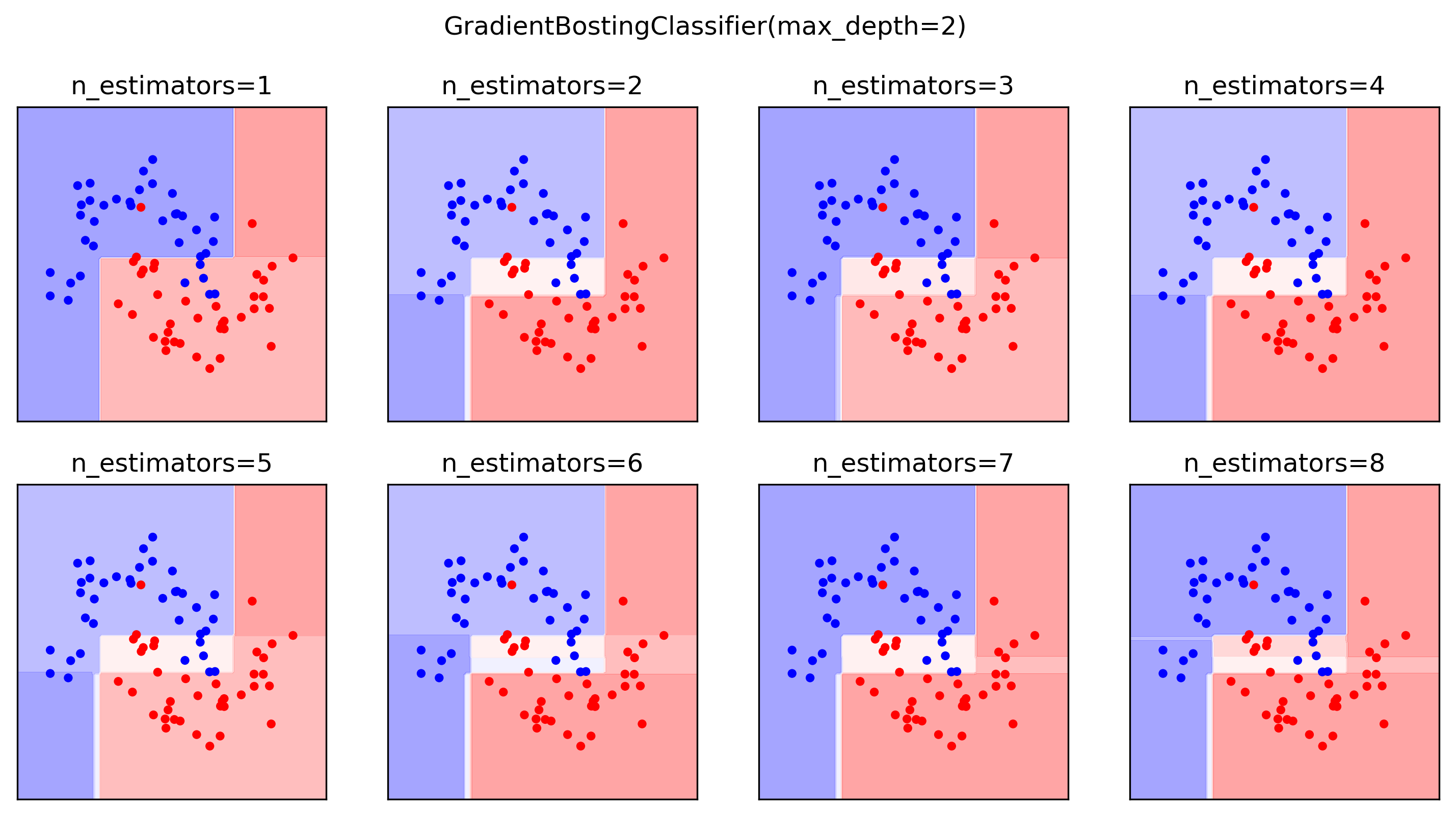 ]
]
Here’s an illustration of what this might look like for classification. This is basically the same thing going on. I’m plotting the probabilities assigned by the model.
Here’s a first estimator, which makes some mistakes here and makes a bunch of mistake in the middle. This is the decision tree of depth two. Then I fit the model to the residuals here. To minimize the log loss of this dataset changes something in the middle, and so on. And you can see that as I add more and more estimator it fits the data better and better and gets more and more complex decision boundaries.
Since it works like a gradient descent on log loss, it’s a little bit harder to visualize this for classification.
White mean probability of 0.5 (which is a tie). Red means high probability for the red class. Blue means a high probability for the blue class. Here, clearly, it hasn’t fit the data perfectly. So I could add more and more models and then, in the end, it would fit the data perfectly.
For multi-class, the default thing to do is One Versus Rest.
Early stopping¶
Adding trees can lead to overfitting
Stop adding trees when validation accuracy stops increasing
two choices:
pick number of trees and tune learning rate
pick learning rate, use early stopping
As I said earlier, if you add more and more trees, the algorithms can overfit. So instead of searching for the learning rate, or searching for number of trees, you can also do early stopping. Because this is a sequential algorithm that gets better and better the more trees you add, you can just use a validation set and stop adding trees once you overfit. You can do that both with scikit-learn and XGBoost.
Basically, the idea is that you pick a large number of estimators and you have a separate validation set and if the validation set accuracy doesn’t improve or if it decreases for number of iterations, say five, then you just stop the learning. This way, you get results faster, because you don’t keep learning but also you possibly get a better model because you know the overfitting.
The only downside stopping learning is that you have fewer data to train your model because you need to the validation set for early stopping. You’ll still need a separate test set to see how well the model actually does. You can’t use the same set for early stopping and for evaluation.
Tuning of Gradient Boosting¶
Typically strong pruning via max_depth
Tune max_features
Tune column subsampling, row subsampling
Regularization
Pick learning rate and do early stopping
Or Pick n_estimators, tune learning rate (if not early stopping)
There are several things you can tune about the gradient boosting. A common approach is to pick the number of estimators that you have time for. So runtime is obviously linear than number of estimators because you need to build each tree one by one. Each tree is built with the same parameters. And then you can tune the learning rate to see how strongly you want to fit the data.
You can also tune something like max features if you want to add more randomness, but that’s actually not very commonly used. You can also subsample the data if you want faster training. And typically there’s a maximum depth. Traditionally, it was like maximum depth of one, two or three, though in kaggle people are doing like 8 to 10 or something. But typically, the depth is much, much smaller than for random forests. This means the model will be small in memory, and also will be faster to predict since you have less deep trees to traverse.
Before we go into implementation I want to talk a little bit about analyzing the models. So again, because it’s a tree-based model, the prediction is a linear combination of trees, you can look at feature importance like the same way we did for random forest and trees.
Improvements:¶
“extreme” gradient boosting¶
Speeding up tree-building via binning¶
Split finding is slow¶
for feature in features:
for threshold in thresholds(f):
gain = compute_gain(feature, threshold)
if gain > best_gain:
best_split = (feature, threshold)
Thresholds: all unique values of feature.
Scanning thresholds = sorting: O(n log n)
Binning features¶
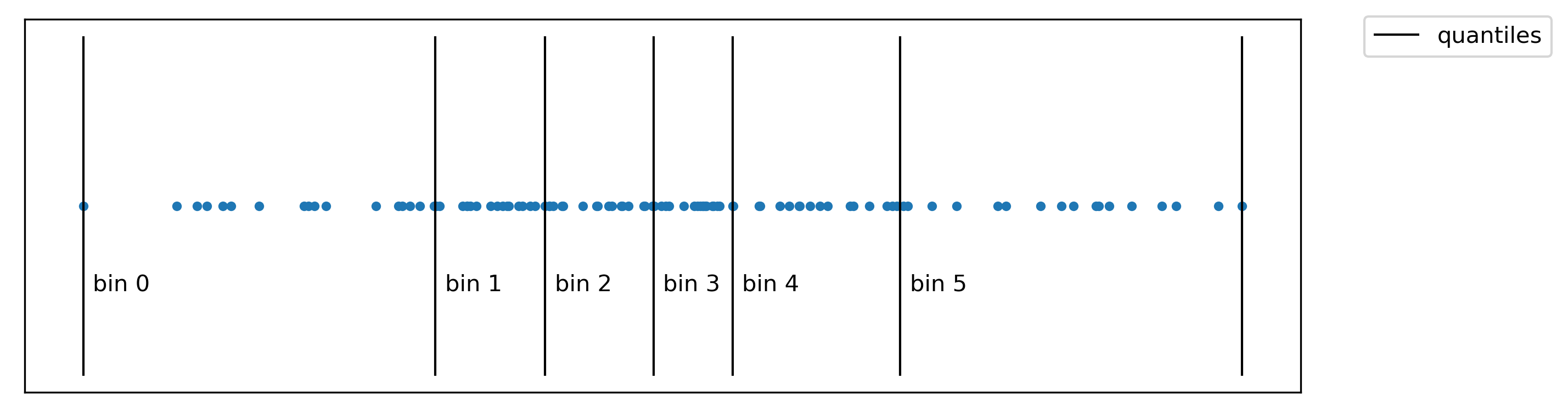
Binning features¶
.left-column[
Original¶
[[5. , 2. , 3.5, 1. ],
[4.9, 3. , 1.4, 0.2],
[4.4, 2.9, 1.4, 0.2],
[5. , 2.3, 3.3, 1. ],
[4.9, 2.5, 4.5, 1.7],
[6.3, 2.5, 5. , 1.9],
[6.3, 2.3, 4.4, 1.3],
[5. , 3.5, 1.3, 0.3],
[6.1, 2.8, 4.7, 1.2],
[5. , 3.5, 1.6, 0.6]])
] .right-column[
Binned¶
[[1, 0, 1, 1],
[0, 2, 0, 1],
[0, 1, 0, 1],
[1, 0, 1, 1],
[0, 0, 2, 3],
[3, 0, 3, 4],
[3, 0, 2, 2],
[1, 4, 0, 1],
[3, 1, 3, 2],
[1, 4, 1, 1]])
]
Binned split finding is fast¶
.left-column[
 ]¶
]¶
.right-column[
 ]
]
A better split criterion¶
Include second order (hessian) and regularizer
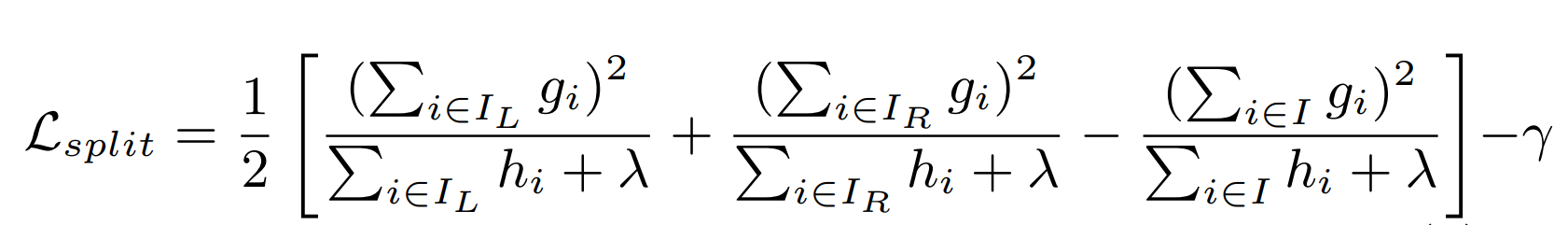
Aggressive sub-sampling¶
.padding-top[ According to user feedback, using column sub-sampling prevents over-fitting even more so than the traditional row sub-sampling. (XGBoost: A Scalable Tree Boosting System, 2016) ]
HistGradientBoostingClassifier¶
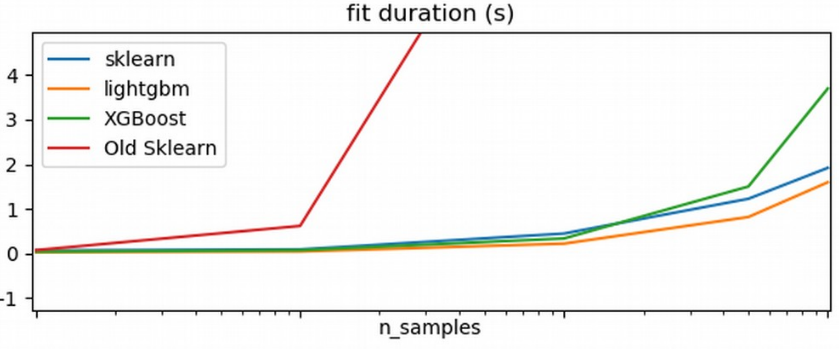
.left-column[
HistGradientBoostingClassifier¶
binning
multicore
no sparse data support
missing value support
soon: monotonicity support
soonish: native categorical variables ]
XGBoost¶
conda install -c conda-forge xgboost
from xgboost import XGBClassifier
xgb = XGBClassifier()
xgb.fit(X_train, y_train)
xgb.score(X_test, y_test))
supports missing values
GPU training
networked parallel training
monotonicity constraints
supports sparse data
In terms of implementation, there’s a couple of implementation methods. Scikit-learn has gradient boosting classifier and gradient boosting regressor. Unfortunately, they are rather slow.
So one of the most commonly used packages is XGBoost, which you can install from conda forge for example. It’s completely scikit-learn compatible. So you can import XGBClassifier if you want you can use it with grid search or with pipelines.
The cool thing is its fast. It supports missing values so you don’t need to do an imputation strategy, you can put them directly into XGBoost. And it also supports multi-core.
The gradient boosting in scikit-learn is just sequential on a single core which on most of the machines are not great. If you have a big machine you want to use all the cores in parallel. You can’t do that with scikit-learn but you can do it with XGBoost.
For random forest, on the other hand, scikit-learn can also run random forest in parallel, because it’s much easier. XGBoost also has a random forest. XGBoost also has some enhancements to the algorithm. It has L1 and L2 penalties for the leaves, so you can do something like an elastic net or lasso penalty to the leaves. I think by default, it’s disabled. But they are not really training like the vanilla decision trees.
One of the reasons they’re faster is because they have a faster implementation. But you can make even faster if you use approximate splits in the trees.
If you want to find a split, you need to search over all features and you need to search over all possible thresholds on the feature. Searching over all possible thresholds on the feature means soaring feature, which is an analog operation. Instead, what you can do is you can bin the features, and then its linear time operation but the threshold will be approximate.
And that will make your computation much faster.
Efficient implementation of gradient boosting (5x sklearn)
Improvements on original algorithm
https://arxiv.org/abs/1603.02754
Adds l1 and l2 penalty on leaf-weights
Fast approximate split finding
Scikit-learn compatible interface
LightGBM¶
conda install -c conda-forge lightgbm
from lightgbm.sklearn import LGBMClassifier
lgbm = LGBMClassifier()
lgbm.fit(X_train, y_train)
lgbm.score(X_test, y_test))
supports missing values
natively supports categorical variables
GPU training
networked parallel training
monotonicity constraints
supports sparse data
CatBoost¶
.smallest[
conda install -c conda-forge catboost
from catboost.sklearn import CatBoostClassifier
catb = CatBoostClassifier()
catb.fit(X_train, y_train)
catb.score(X_test, y_test))
] .smaller[
optimized for categorical variables
uses one feature / threshold for all splits on a given level aka symmetric trees
Symmetric trees are “different” but can be much faster
supports missing value
GPU training
monotonicity constraints
uses bagged and smoothed version of target encoding for categorical variables
lots of tooling ]
Gradient Boosting Advantages¶
Very fast using HistGradientBoosting (or XGBoost, LightGBM)
Small model size
Typically more accurate than Random Forests
“old” GradientBoosting in sklearn is comparatively slow
It’s sort of slower to train if you’re training serial, but if you paralyze it, it’s often faster to train since it has a much smaller model size. So the trees are usually not as deep and you don’t need as many because you’re doing much more focused learning where you try to correct the mistakes of the other models. So usually it’s very fast to predict because prediction can happen in parallel over all the trees, while learning cannot happen in parallel over all the trees necessarily. Usually, this is more accurate than random forests.
The question is for the same number of estimators, how does low versus high learning rate changes?
High learning rate allows you to fit the data more strongly and also overfit the data more strongly.
Concluding tree-based models¶
When to use tree-based models¶
Model non-linear relationships
Doesn’t care about scaling, no need for feature engineering
Single tree: very interpretable (if small)
Random forests very robust, good benchmark
Gradient boosting often best performance with careful tuning
To summarize, tree-based models are really very, very popular family of models. They’re very commonly used. You probably want to use them if you want nonlinear relationships, or if you have a lot of different kinds of weird features because they really don’t care about scaling of the features, so it allows you to get rid of mostly preprocessing.
If you want very interpretable model, single trees or small single trees are good ideas, because it’s one of the few models that you can sort of write down on a blackboard and show to someone, and they’ll have some idea of what’s going on. That’s impossible for any other models.
Random forests are great because they’re very robust. And you don’t have to tune anything, you just run a random forest with 100 trees and with the default settings and it will work great.
And so this one of my first benchmarks. Usually, I first ran a logistic regression then I run random forests.
Gradient Boosting is often the best performing model, sort of the centered toolbox. Sometimes you need to tune a little bit more, so you need to tune the depth of the trees or the learning rate, and so on. But if you tune them, then they will usually beat random forest on those data sets.
One case where you might not want to use trees is if you have very high dimensional sparse data then linear models might work better but also your mileage may vary. On the contrary, if you have like a low dimensional space, tree-based models are probably a good bet.
Next thing we’ll talk about is a different way to build ensembles, different way to put together multiple models.
from sklearn.ensemble import GradientBoostingClassifier
from sklearn.datasets import load_breast_cancer
from sklearn.model_selection import train_test_split
cancer = load_breast_cancer()
X_train, X_test, y_train, y_test = train_test_split(
cancer.data, cancer.target, random_state=0)
gbrt = GradientBoostingClassifier(random_state=0)
gbrt.fit(X_train, y_train)
print("accuracy on training set: %f" % gbrt.score(X_train, y_train))
print("accuracy on test set: %f" % gbrt.score(X_test, y_test))
gbrt = GradientBoostingClassifier(random_state=0, max_depth=1)
gbrt.fit(X_train, y_train)
print("accuracy on training set: %f" % gbrt.score(X_train, y_train))
print("accuracy on test set: %f" % gbrt.score(X_test, y_test))
gbrt = GradientBoostingClassifier(random_state=0, learning_rate=0.01)
gbrt.fit(X_train, y_train)
print("accuracy on training set: %f" % gbrt.score(X_train, y_train))
print("accuracy on test set: %f" % gbrt.score(X_test, y_test))
gbrt = GradientBoostingClassifier(random_state=0, max_depth=1)
gbrt.fit(X_train, y_train)
plt.barh(range(cancer.data.shape[1]), gbrt.feature_importances_)
plt.yticks(range(cancer.data.shape[1]), cancer.feature_names);
ax = plt.gca()
ax.set_position([0.4, .2, .9, .9])
from xgboost import XGBClassifier
xgb = XGBClassifier()
xgb.fit(X_train, y_train)
print("accuracy on training set: %f" % xgb.score(X_train, y_train))
print("accuracy on test set: %f" % xgb.score(X_test, y_test))
from xgboost import XGBClassifier
xgb = XGBClassifier(n_estimators=1000)
xgb.fit(X_train, y_train)
print("accuracy on training set: %f" % xgb.score(X_train, y_train))
print("accuracy on test set: %f" % xgb.score(X_test, y_test))
Exercise¶
Use GradientBoostingRegressor on the Bike dataset.
Search over the learning_rate and max_depth using GridSearchCV.
What happens if you change n_estimators?
Compare the speed of XGBClassifier with GradientBoostingRegressor. How well does XGBClassifier do with defaults on the Bike dataset? Can you make it do better?